t-SNE
t-SNE在应用中主要作为数据可视化的一种手段而不作为降维的手段, 主要是因为其时间复杂度太高, 同时降维后损失的信息太多. 这篇文章主要总结一下t-SNE的笔记.
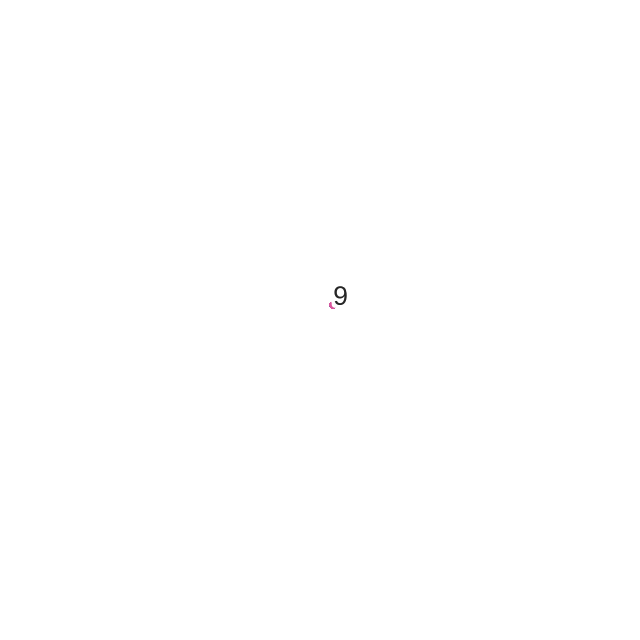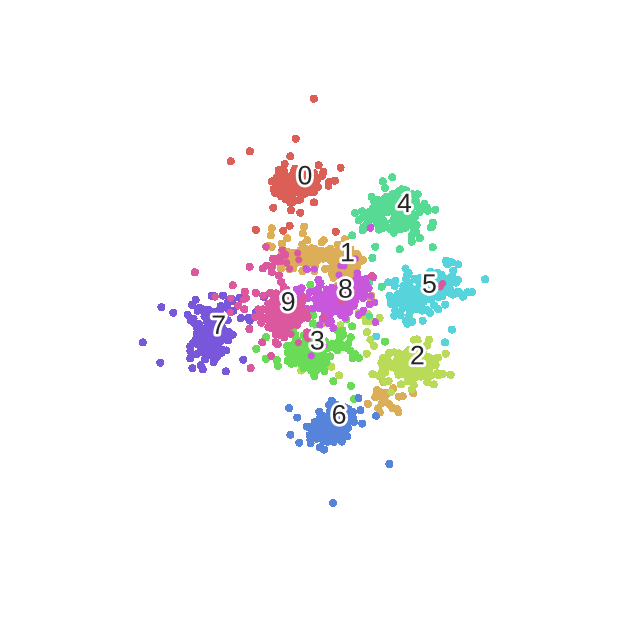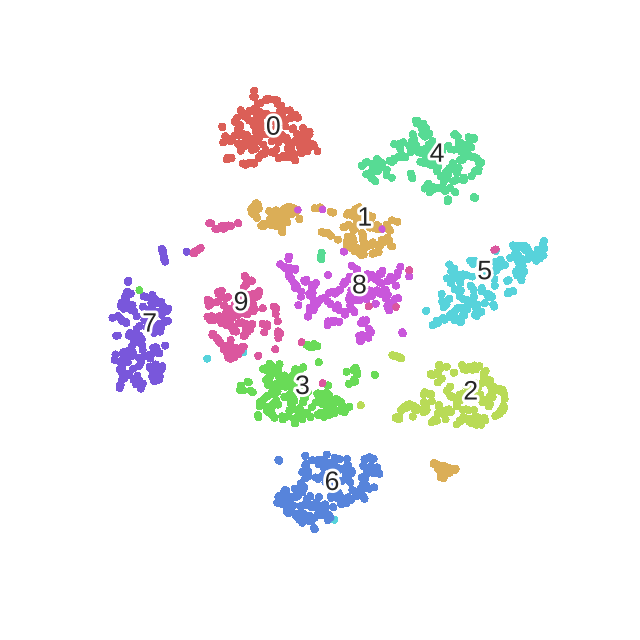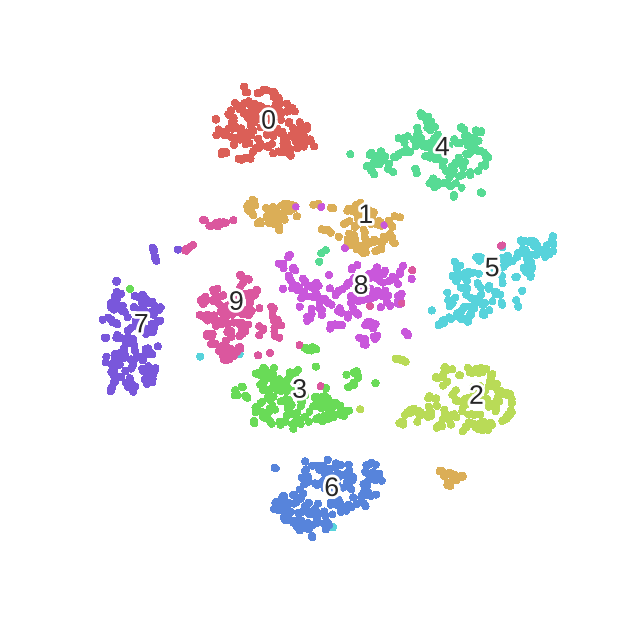
简介
t-SNE is a tool for data visualization. It reduces the dimensionality of data to 2 or 3 dimensions so that it can be plotted easily. Local similarities are preserved by this embedding.
t-SNE converts distances between data in the original space to probabilities. First, we compute conditional probabilites
$$p_{j|i} = \frac{\exp{(-d(\boldsymbol{x}_i, \boldsymbol{x}_j) / (2 \sigma_i^2)})}{\sum_{i \neq k} \exp{(-d(\boldsymbol{x}_i, \boldsymbol{x}_k) / (2 \sigma_i^2)})}, \quad p_{i|i} = 0,$$
which will be used to generate joint probabilities
$$p_{ij} = \frac{p_{j|i} + p_{i|j}}{2N}.$$
The $\sigma_i$ will be determined automatically. This procedure can be influenced by setting the perplexity of the algorithm.
A heavy-tailed distribution will be used to measure the similarities in the embedded space
$$q_{ij} = \frac{(1 + ||\boldsymbol{y}_i - \boldsymbol{y}_j)||^2)^{-1}}{\sum_{k \neq l} (1 + ||\boldsymbol{y}_k - \boldsymbol{y}_l)||^2)^{-1}},$$
and then we minimize the Kullback-Leibler divergence
$$KL(P|Q) = \sum_{i \neq j} p_{ij} \log \frac{p_{ij}}{q_{ij}}$$
between both distributions with gradient descent (and some tricks). Note that the cost function is not convex and multiple runs might yield different results.
下面是sklearn的TSNE注释, 很不错的说明了算法流程和实际使用的trick.
class TSNE(sklearn.base.BaseEstimator)
| t-distributed Stochastic Neighbor Embedding.
|
| t-SNE [1] is a tool to visualize high-dimensional data. It converts
| similarities between data points to joint probabilities and tries
| to minimize the Kullback-Leibler divergence between the joint
| probabilities of the low-dimensional embedding and the
| high-dimensional data. t-SNE has a cost function that is not convex,
| i.e. with different initializations we can get different results.
|
| It is highly recommended to use another dimensionality reduction
| method (e.g. PCA for dense data or TruncatedSVD for sparse data)
| to reduce the number of dimensions to a reasonable amount (e.g. 50)
| if the number of features is very high. This will suppress some
| noise and speed up the computation of pairwise distances between
| samples. For more tips see Laurens van der Maaten's FAQ [2].
|
| >>> import numpy as np
| >>> from sklearn.manifold import TSNE
| >>> X = np.array([[0, 0, 0], [0, 1, 1], [1, 0, 1], [1, 1, 1]])
| >>> model = TSNE(n_components=2, random_state=0)
| >>> model.fit_transform(X) # doctest: +ELLIPSIS, +NORMALIZE_WHITESPACE
| array([[ 887.28..., 238.61...],
| [ -714.79..., 3243.34...],
| [ 957.30..., -2505.78...],
| [-1130.28..., -974.78...])
降维
降维顾名思义就是把数据或特征的维数降低,一般分为线性降维和非线性降维,比较典型的如下:
线性降维:PCA(Principal Components Analysis)、LDA(Linear Discriminant Analysis)、MDS(Classical Multidimensional Scaling)
非线性降维:Isomap(Isometric Mapping)、LLE(Locally Linear Embedding)、LE(Laplacian Eigenmaps) 大家可能对线性降维中的一些方法比较熟悉了,但是对非线性降维并不了解,非线性降维中用到的方法大多属于流形学习方法。
流形学习
现在的$AI$有两个意思,一个广义的$AI$,包括了所有相关的以及派生的领域,另一个则是狭义的或者经典的$AI$,专门指那些仍然在执着地追求着真正的“智能”的部分(比如符号推导),或者说得不好听一点,就是剩下的部分.
机器学习相比经典的AI可能有很多的不同, 更像应用数学, 或者说数学建模, 根据已有的数据, 由一些已有的经验的假设, 我们可以构建一个模型, 这个模型会有一些参数(即使没有参数, 也可以类似的看待), 然后根据数据来求解模型, 这样一个过程我们称为learning.
接下来谈到流形, 流形学习(Manifold Learning)听名字就觉得非常深奥,涉及微分流行和黎曼几何等数学知识, 直观上来讲,一个流形好比是一个$d$维的空间,在一个$m$维的空间中 ($m$ > $d$) 被扭曲之后的结果, 实际上流形学习就是添加了对数据的流形假设的学习。当然,想要了解流形学习并不需要我们一行一行的去推导公式,通过简单的例子也能够有一个直观的认识。关于流行学习的科普文章首推pluskid写的《浅谈流行学习》,里面有很多通俗易懂的例子和解释, 这里的流形实际上就是一个空间, 实际上流形学习就是学习低位表征, 因为虽然一个数据是高维的, 但是真正表达其含义的更有效的表征可能是嵌入在低维空间的.
SNE
What?
- SNE是一种用来将高维数据隐射到低维数据的概率映射, 特点是映射后保留近邻特性.
- 用高斯分布来对近邻特性进行建模.
- embedding的优化目标是在低维空间尽可能的近似高维空间的近邻特性.
Why?
- 自动降维在ML中很重要
- PCA, LLE, GTM等老方法都是确定性的映射, 因此对于一些比较模糊的对象效果就不是那么好了.
How?
$x_i,x_j$的近邻可能性如下
$$p_{ij} = \frac{e^{-d_{ij}^2}}{\sum_{k\neq i}e^{-d_{ij}^2}}$$
其中$d_{ij} = \frac{||x_i-x_j||^2}{2\sigma_i^2}$, $\sigma_i$是自己选择的参数, 可以看作有效邻居范围.
映射后, 在低维空间, 有$y_i,y_j$, 同样的我们可以得到近邻概率.
$$q_{ij} = \frac{e^{-d_{ij}^2}}{\sum_{k\neq i}e^{-d_{ij}^2}}$$
其中$d_{ij} = ||x_i-x_j||^2$.
由于这是概率分布, 我们用KL散度来计算两者之间的差异.
$$C=\sum_iKL(P_i||Q_i)=\sum_i\sum_jp_{ij}log\frac{p_{ij}}{q_{ij}}$$
此时只需要利用梯度下降进行求解即可
$$\frac{ {\partial}C}{ {\partial}y_i}=2\sum_j(p_{ij}-q_{ij}+p_{ji}-q_{ji})(y_i-y_j)$$
此处的梯度可以用分子的引力和斥力来理解. 具体其他点某个点的作用力是引力还是斥力是由两者的距离决定的, 这里可以由$(p_{ij}-q_{ij}+p_{ji}-q_{ji})$进行反应.
Results
在UBS数据上使用上述算法, 有以下结果.

结论
- 无监督的情况下可以很好的对数据进行分离.
- 各类之间的边界太模糊.
t-SNE
解决不对称性
为了对SNE进行改进, 首先解决近邻概率的不对称性, 这是因为不对称性导致映射后任然保持的是局部的结构而不是全局的一个特征.
此处利用求均值来解决.
$$p_{ij} = \frac{p_{ij}+p_{ji}}{2n}$$
此时梯度有
$$\frac{ {\partial}C}{ {\partial}y_i}=2\sum_j(p_{ij}-q_{ij})(y_i-y_j)$$
相比刚才定义的公式,这个梯度更加简化,计算效率更高。但是别高兴的太早,虽然我们解决了SNE中的不对称问题,得到了一个更为简单的梯度公式,但是Maaten指出,对称SNE的效果只是略微优于原始SNE的效果,依然没有从根本上解决问题。
解决拥挤问题
所谓拥挤问题,顾名思义,看看SNE的可视化效果,不同类别的簇挤在一起,无法区分开来,这就是拥挤问题。有的同学说,是不是因为SNE更关注局部结构,而忽略了全局结构造成的?这的确有一定影响,但是别忘了使用对称SNE时同样存在拥挤问题。实际上,拥挤问题的出现与某个特定算法无关,而是由于高维空间距离分布和低维空间距离分布的差异造成的, 这主要是由维数爆炸问题造成的, 在高维空间很稀疏的分布映射到低维空间就会变得很密集, 这里可以由在球体内均匀分布的点来表示, 随着维度的上升, 大部分的点都将集中在球表面, 这是因为球表面附近代表的空间增大的速度远大于内部空间增长的速度.
我们生活在一个低维的世界里,所以有些时候思维方式容易受到制约。比如在讨论流形学习问题的时候,总喜欢拿一个经典的“Swiss roll”作为例子,这只不过是把一个简单的二维流形嵌入到三维空间里而已。实际上真实世界的数据形态远比“Swiss roll”复杂,比如一个10维的流形嵌入到更高维度的空间中,现在我们的问题是把这个10维的流形找出来,并且映射到二维空间上可视化。在进行可视化时,问题就来了,在10维流形上可以存在11个点且两两之间距离相等。在二维空间中呢?我们最多只能使三个点两两之间距离相等,想将高维空间中的距离关系完整保留到低维空间是不可能的。

t-分布
t-分布具有长尾特性, 相比高斯分布对异常点的抗干扰能力更强, 在没有异常点的时候和高斯分布的拟合结果基本一致. 在解决上, 我们让高斯分布对应高维空间, t-分布对应地维空间, 如下图所示.

可以看到那么对于高维空间中相距较近的点,为了满足$p_{ij}=q_{ij}$,低维空间中的距离需要稍小一点;而对于高维空间中相距较远的点,为了满足$p_{ij}=q_{ij}$,低维空间中的距离需要更远。 这样正好就使得在低维空间中同类的聚合的更加紧密, 不同类的点更加疏远了. 我们使用自由度为1的t分布来定义$q_{ij}$
$$q_{ij}=\frac{(1+||y_i-y_j||^2)^{-1}}{\sum_{k\neq l}(1+||y_k-y_l||^2)^{-1}}$$
损失仍然用KL散度, 此时梯度变为
$$\frac{ {\partial}C}{ {\partial}y_i}=4\sum_j(p_{ij}-q_{ij})(y_i-y_j)(1+||y_i-y_j||^2)^{-1}$$
具体的算法如下

总结
所谓的t-SNE算法,总结一下其实就是在SNE的基础上增加了两个改进:一是把SNE变为对称SNE,二是在低维空间中采用了tt分布代替原来的高斯分布,高维空间不变。
下面是论文的和其他流行学习方法进行的比较

最后是在MNIST数据上训练的迭代过程.
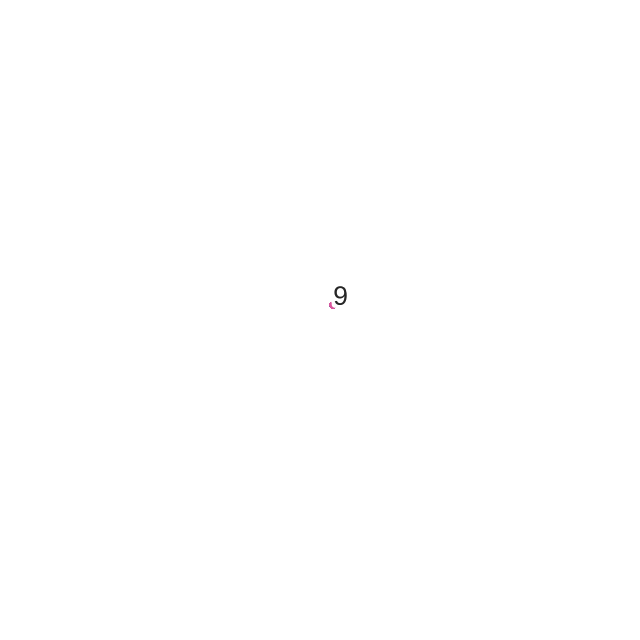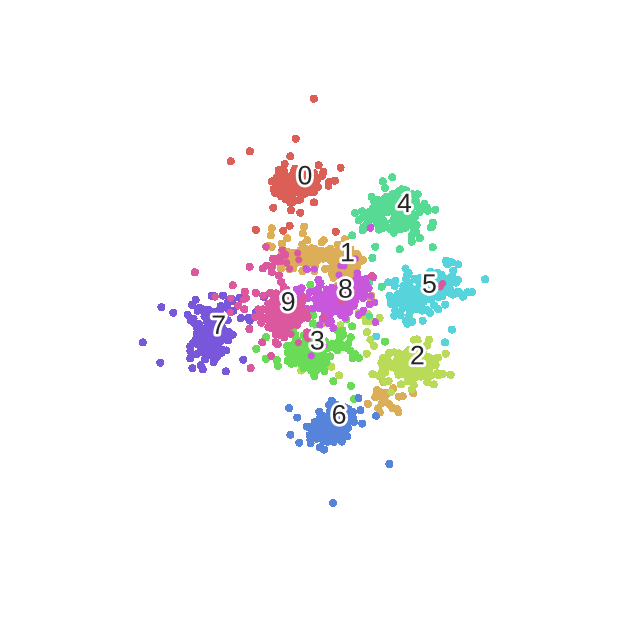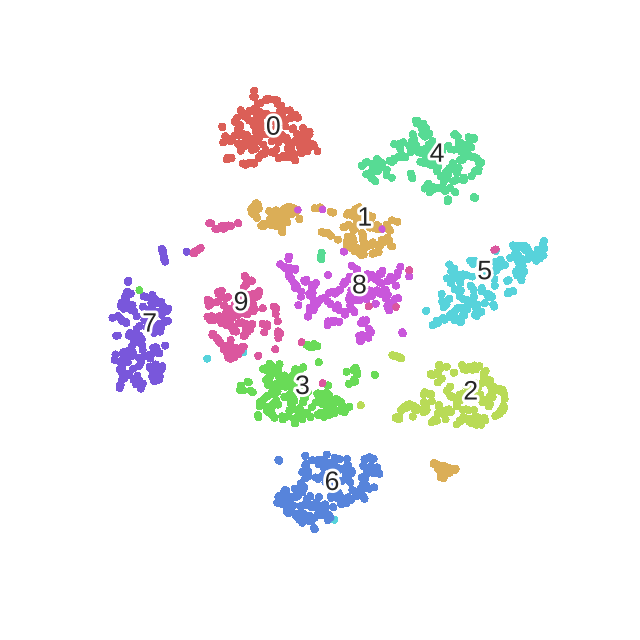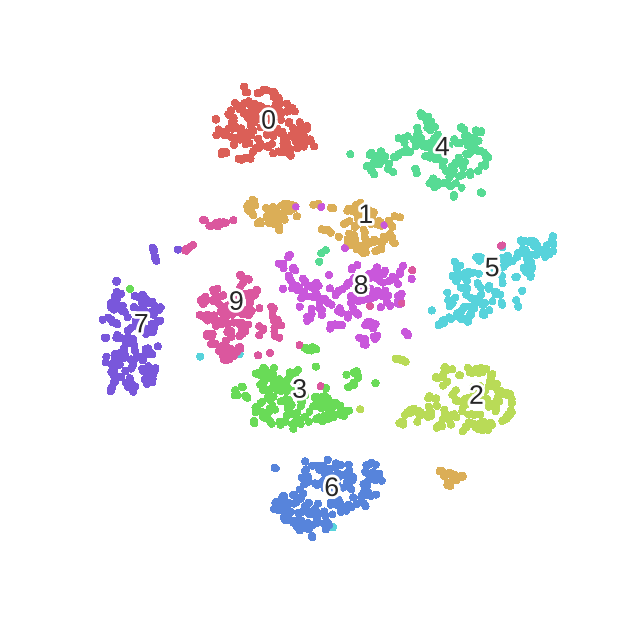
需要注意的是t-SNE有两个缺点
- 训练时间过长
- 参数对不同数据集比较敏感, 调参比较麻烦.
改进方向
KNN近邻
在计算近邻概率的时候需要计算全部的数据, 这很花时间, 因此可以只计算最近的k的概率, 这里就需要构建knn图, 有一种VP树(vantage-point tree)来构建这个kNN图,可以在$O(uNlogN)$的时间复杂度内得到一个精确的kNN图。
梯度中斥力的近似
LargeVIS
唐建提出的LargeVis基本思路与t-SNE改进算法大致相同,如下图所示:

LargeVis的主要不同是用到了几个非常漂亮的优化技巧.
高效kNN图构建算法
这里不同于VP树, 构建kNN图一般有三类方法,第一类是空间分割树(space-partitioning trees)算法,第二类是局部敏感哈希(locality sensitive hashing)算法,第三类是邻居搜索(neighbor exploring techniques)算法。其中k-d树和随机投影树均属于第一类算法。
LargeVis的做法是将第一类方法和第三类方法相结合。具体来说,第一步先利用随机投影树得到一个空间划分,在此基础上寻找每个点的kk近邻,得到一个初步kNN图,这个kNN图不要求完全准确。第二步根据“邻居的邻居可能也是我的邻居”的思想,利用邻居搜索算法寻找潜在的邻居,计算邻居与当前点、邻居的邻居与当前点的距离并放入一个小根堆之中,取距离最小的k个节点作为k近邻,最终得到一个精确的kNN图。
新的损失函数
LargeVis在近邻图的基础上对损失函数进行了很多修改,整个优化目标很好理解,就是最大化正样本的节点对在kNN图中有连接边的概率,最小化负样本的节点对在kNN图中有连接边的概率,其中$γ$是我们统一为负样本边设定的权值。这里再取一个对数,优化目标变为:
$O=\sum_{(i,j)\in E}w_{ij}p(e_{ij}=1)\sum_{i,j\in \hat E}γ(1-p(e_{ij}=1))$
同时引入了负采样(解决负样本过多), 边采样(解决梯度梯度消失和剧增问题), 异步随机梯度下降(对稀疏图很有效)来进行训练上的改善. 下面是实验上的结果.

LargeVis一般的效果和t-SNE的效果差不多, 但是训练时间可以得到非常大的提升.

实现-pytorch
这里用pytorch从0实现一个t-SNE.
Reference
An illustrated introduction to the t-SNE algorithm
Visualizing Data Using t-SNE
t-distribution
from-sne-to-tsne
t-SNE
浅谈流形学习
word2vec
Hinton G E, Roweis S T. Stochastic neighbor embedding[C]//Advances in neural information processing systems. 2002: 833-840.
Van der Maaten L, Hinton G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9(2579-2605): 85.
Accelerating t-SNE using Tree-Based Algorithms