ANNS
本文主要总结了ANNS(近似最近邻搜索)的常用方法, 并实现了一个p-stable LSH, 与开源库FLANN在SIFT1M和GIST1M数据上进行了性能比较试验. 本文代码已经上传至 github 上.

常用的方法
从宏观上, brute-force搜索的方式是在全空间进行搜索,为了加快查找的速度,几乎所有的ANN方法都是通过对全空间分割,将其分割成很多小的子空间,在搜索的时候,通过某种方式,快速锁定在某一(几)子空间,然后在该(几个)子空间里做遍历。
一般近似最近邻的方法主要有三种
基于分割树的方法.
这一类方法的主要的特征是对空间进行划分.
- kd-tree.
- 随机kd-tree(多个并行树, 随机选择方差最大的k个维度), 实际中这个比较好用.
- 随机投影树(多个维度分割, 不只是一个维度).
- 优先搜索k-means搜索树, 与kd-tree不同的在于其分割是基于k-means算法, 而不是单一维度, 具体算法是先对数据进行k-means划团, 然后递归的对每一个团进行k-means划分, 直到团内点的个数少于k, 算法如下.
- PQ乘积量化也属于分割方法的一种.
对KD树选择从哪一维度进行开始划分的标准,采用的是求每一个维度的方差,然后选择方差最大的那个维度开始划分。这里有一个比较有意思的问题是:为何要选择方差作为维度划分选取的标准?我们都知道,方差的大小可以反映数据的波动性。方差大表示数据波动性越大,选择方差最大的开始划分空间,可以使得所需的划分面数目最小,反映到树数据结构上,可以使得我们构建的KD树的树深度尽可能的小。

一般而言,在空间维度比较低的时候,KD树是比较高效的,当空间维度较高时,可以采用下面的哈希方法或者矢量量化方法。
kd-trees are not suitable for efficiently finding the nearest neighbour in high dimensional spaces.
In very high dimensional spaces, the curse of dimensionality causes the algorithm to need to visit many more branches than in lower dimensional spaces. In particular, when the number of points is only slightly higher than the number of dimensions, the algorithm is only slightly better than a linear search of all of the points.
PQ乘积量化
这里对PQ方法做一个笔记, PQ乘积量化的核心思想还是聚类,或者说具体应用到ANN近似最近邻搜索上,K-Means是PQ乘积量化子空间数目为1的特例。PQ乘积量化生成码本和量化的过程可以用如下图示来说明:

在训练阶段,针对N个训练样本,假设样本维度为128维,我们将其切分为4个子空间,则每一个子空间的维度为32维,然后我们在每一个子空间中,对子向量采用K-Means对其进行聚类(图中示意聚成256类),这样每一个子空间都能得到一个码本。这样训练样本的每个子段,都可以用子空间的聚类中心来近似,对应的编码即为类中心的ID。如图所示,通过这样一种编码方式,训练样本仅使用的很短的一个编码得以表示,从而达到量化的目的。对于待编码的样本,将它进行相同的切分,然后在各个子空间里逐一找到距离它们最近的类中心,然后用类中心的id来表示它们,即完成了待编码样本的编码。
正如前面所说的,在矢量量化编码中,关键是码本的建立和码字的搜索算法,在上面,我们得到了建立的码本以及量化编码的方式。剩下的重点就是查询样本与dataset中的样本距离如何计算的问题了。
在查询阶段,PQ同样在计算查询样本与dataset中各个样本的距离,只不过这种距离的计算转化为间接近似的方法而获得。PQ乘积量化方法在计算距离的时候,有两种距离计算方式,一种是对称距离,另外一种是非对称距离。非对称距离的损失小(也就是更接近真实距离),实际中也经常采用这种距离计算方式。下面过程示意的是查询样本来到时,以非对称距离的方式(红框标识出来的部分)计算到dataset样本间的计算示意:

具体地,查询向量来到时,按训练样本生成码本的过程,将其同样分成相同的子段,然后在每个子空间中,计算子段到该子空间中所有聚类中心得距离,如图中所示,可以得到4*256个距离,这里为便于后面的理解说明,小白菜就把这些算好的距离称作距离池。在计算库中某个样本到查询向量的距离时,比如编码为(124, 56, 132, 222)这个样本到查询向量的距离时,我们分别到距离池中取各个子段对应的距离即可,比如编码为124这个子段,在第1个算出的256个距离里面把编号为124的那个距离取出来就可,所有子段对应的距离取出来后,将这些子段的距离求和相加,即得到该样本到查询样本间的非对称距离。所有距离算好后,排序后即得到我们最终想要的结果。
从上面这个过程可以很清楚地看出PQ乘积量化能够加速索引的原理:即将全样本的距离计算,转化为到子空间类中心的距离计算。比如上面所举的例子,原本brute-force search的方式计算距离的次数随样本数目N成线性增长,但是经过PQ编码后,对于耗时的距离计算,只要计算4*256次,几乎可以忽略此时间的消耗。另外,从上图也可以看出,对特征进行编码后,可以用一个相对比较短的编码来表示样本,自然对于内存的消耗要大大小于brute-force search的方式。
基于哈希函数
基于local sensitive hash, 这些哈希函数的特征是数据足够接近的时候, 数据对应的哈希值也会足够近, 需要基于距离测量函数, 选择不同的哈希函数, 在需要保证recall的情况下, 几乎等同于线性搜索, 主要依赖哈希函数的选择. 注意multiprobe多探头, 就是在查询样本所在的哈希通附近以汉明距离下查找邻近的哈希桶. 这样LSH在任意一个哈希表中查找到最近邻的概率变得更高,从而使得我们能到减少哈希表的构建数目, 进而减少使用的内存.
近邻图技巧
主要思想是构建近邻图结构, 对query进行近邻搜索, 即邻居的邻居很有可能也是我的邻居, 需要构建knn树.
Local sensitive hash
LSH(local sensitive hash)
$(d_1,d_2,p_1,p_2)$ - 敏感:
- $d(x,y){\leq}d_1$, 则 $f(x)=f(y)$ 概率至少为 $p_1$.
- $d(x,y){\geq}d_2$, 则 $f(x)=f(y)$ 概率至多为$p_2$.
- 不同的距离函数对应不同的LSH函数族.
- 函数族之间有不同的 $(d_1,d_2,p_1,p_2)$ 敏感性.
- 对一个LSH函数族 $F$, 进行放大处理为 $F’$, 以降低假阳( FP ), 假阴( FN ), 代价是增大了计算时间. $F’$ 的定义为: $F’$ 的每一个成员函数是由 $r$ 个 $F$ 的成员函数构成.
常见的距离与其对应的函数族
- Jaccard 距离对应 $(d_1,d_2,1-d_1,1-d_2)$ LSH 函数族.
- 海明距离对应 $(d_1,d_2,1-d_1/d,1-d_2/d)$LSH 函数族, 除以 $d$ 以归一化为概率.
- 余弦距离对应 $(d_1,d_2,\frac{180-d_1}{180}, \frac{180-d_2}{180})$LSH 函数族, 除以 180 以归一化为概率. 基于随机平面投影.
- 2维欧式距离对应 $(\frac{a}{2},2a,\frac{1}{2},\frac{1}{3})$LSH 函数族, 需要定义 $a$. 基于随机直线投影, 可以进而推广到多维.
FLANN中的LSH浮点数实现
FLANN 中只有海明距离的实现, 先把原数据预处理到海明空间后再建立索引, 因此只能接受整数数据, 想接受浮点数据, 也就是不进行预处理, 应该采用 p-stable LSH. 找到了一个含有 p-stable 的开源实现$E^2LSH$, 包含欧式和海明空间.
p-stable 分布及 p-stable LSH
定义: 随机变量 $X$ 满足对任意的向量 $v$, 有$\sum_iv_iX_i$ 与 $||v||_pX$ 具有相同的分布, 则 $X$ 为 p-stable 分布.
p-stable 分布重要的应用就是可以估计给定向量 $v$ 的 p 范数 $||v||_p$.
在LSH中是反过来用 $(v_1-v_2)a$ 来近似 $||v_1-v_2||pX$, 此时就可以定义出相应的哈希函数族$h{a,b}(v)=[\frac{av+b}{w}]$, 其中$av$表示映射到一条直线上, 然后加$b$除以$w$以分段近似为整数, 依旧是保留了部分信息.
具体实现方法
对每一个独立的哈希表, 计算每一个向量$v$对其的键值算法如下.
- 由正态分布$N(0,1)$生成k个向量$a$, 每个向量$a$的维度与输入向量$v$的维度一致, 计算$a*v$, 生成k个哈希值, 对每一个哈希值按照其正负性映射为0,1, 然后按照二进制数连接起来, 获取到哈希表对应的哈希键值.
具体索引相似项时, 因为只是对全部一样的加入候选集会导致候选集过小, 所以计算汉明距离小于等于1的哈希键值对应的项都加入候选集内.
实现
硬件
- Macbook Pro 2014 mid
- CPU: Intel Core i5, 3.30GHz, 8GB RAM
实验结果
对每一种算法, 在固定精度下, 对平均每秒能够进行的近似搜索次数进行计算, 同时由于尺度问题, 对y轴即搜索性能采用的是对数坐标轴, 画出下面实验结果.
SIFT1M Dataset
Precision-Performance tradeoff - up and to the right is better
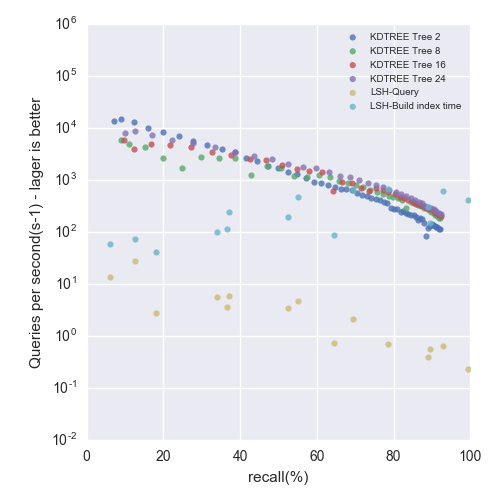
Figure 1: SIFT1M dataset
| The number of trees | Build index time | Peak memory |
|---|---|---|
| 2 | 3.9 s | 689.0 MB |
| 8 | 16.5 s | 1046.7 MB |
| 16 | 34.8 s | 1218.9 MB |
| 24 | 49.3 s | 1560.0 MB |
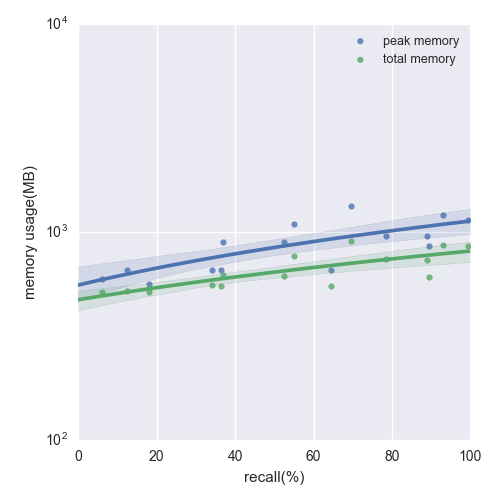
Figure 2: The memory usage of LSH in building the index for SIFT1M dataset
GIST1M Dataset
Precision-Performance tradeoff - up and to the right is better
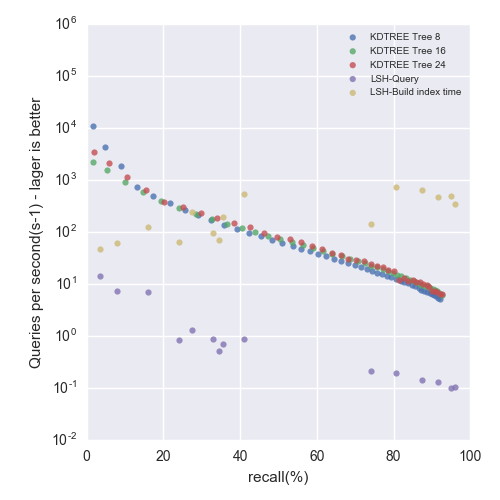
Figure 3: GIST1M dataset
| The number of trees | Build index time | Peak memory |
|---|---|---|
| 8 | 64.9 s | 4184.2 MB |
| 16 | 113.9 s | 4687.7 MB |
| 24 | 175.8 s | 5176.0 MB |

Figure 4: The memory usage of LSH in building the index for GIST1M dataset
结论
- 可以看到两个算法总体上在中间一段是近似对数线性的, 而在两端则变化较快, 精度要求越高, 近似搜索的速度也就越慢.
- flann的kdtree算法的性能在SIFT和GIST数据集上优于我实现的p-stable LSH的.
- 随着并行树数目的增多, KDTREE算法建立索引时的峰值内存使用也会增多.
- 随着精度要求的增大, 在并行树的数目足够多的情况下, KDTREE建索引的时间不会有太大的影响. 这是由于KDTREE算法精度主要依赖于checks数目, 而建索引时间主要受并行树数目决定.
- 随着精度要求的增大, LSH算法建索引的时间也会随之增大, 同时其建索引阶段所占的峰值内存和建立好后索引数据结构本身所占的内存也会随之增大.
Reference
Scalable Nearest Neighbor Algorithms for High Dimensional Data
flann
flann user manual
Mining of Massive Datasets cp3
Locality-Sensitive Hashing for Finding Nearest Neighbors
LSH和p-stable LSH
$E^2LSH$
$E^2LSH$ user manual
图像检索:再叙ANN Search