Machine learning notes

一些机器学习tips的笔记, 可能会比较杂, 持续更新..
会看的书有
- 统计学习方法 - 李航
- 深入理解机器学习 - Shai
- 机器学习 - Peter Flach
生成模型与判别模型的区别
有监督机器学习方法可以分为生成方法和判别方法(常见的生成方法有混合高斯模型、朴素贝叶斯法和隐形马尔科夫模型等,常见的判别方法有SVM、LR等),生成方法学习出的是生成模型,判别方法学习出的是判别模型。
生成方法由数据学习出联合概率密度, 然后求出条件概率密度, 判别模型直接学习条件概率或者判别函数.
贝叶斯和概率学派有什么区别
贝叶斯相比概率学派保留了不确定性, 比如我们把概率推断和贝叶斯推断都看做一个函数, 输入是统计问题, 那么概率推断输出的是一个确定的参数, 而贝叶斯推断输出的是随机变量, 比如我们写了一段代码, 我们会提出一个问题, 这段代码有bug吗, 概率学派可能会回答, 有bug, 但是贝叶斯学派就会回答, 你的代码有80%的概率有bug, 20%的概率没有bug. 这就是主要的区别.
MCMC方法
MCMC方法主要是用来进行贝叶斯推断的计算工具, 用来近似求解最大后验参数. 比如我们把整个概率模型建立好了后, 也就是先验概率建立好了, 输入我们的证据也就是数据, 就可以用MCMC来求解后验概率最大的参数.
大数定理和中心极限定理
大数定理是指服从同一分布的随机变量的均值, 收敛于该分布的均值.
中心极限是指独立的随机变量之和服从高斯分布.
余弦相似性和皮尔逊相关系数的关系
皮尔逊相关系数就是减去平均值(中心化)后做余弦相似性

- 如果数据密集(所有数据几乎都有属性值,属性值量级重要),就用欧几里德算法
- 数据受级别膨胀影响(不同的用户使用不同的评分标准),就用皮尔逊相关系数算法
- 数据稀疏性强,就考虑用夹角余弦相似度算法
余弦相似性值只考虑方向夹角, 但是欧式距离考虑距离, 会受到标度的影响, 因此一般要进行标准化.
Bias 与 Variance

Error = Bias + Variance + Noise
参考 维基百科
推导过程
准: bias描述的是根据样本拟合出的模型的输出预测结果的期望与样本真实结果的差距,简单讲,就是在样本上拟合的好不好。要想在bias上表现好,low bias,就是复杂化模型,增加模型的参数,但这样容易过拟合 (overfitting),过拟合对应上图是high varience,点很分散。low bias对应就是点都打在靶心附近,所以瞄的是准的,但手不一定稳。
确: varience描述的是样本上训练出来的模型在测试集上的表现,要想在varience上表现好,low varience,就要简化模型,减少模型的参数,但这样容易欠拟合(unfitting),欠拟合对应上图是high bias,点偏离中心。low varience对应就是点都打的很集中,但不一定是靶心附近,手很稳,但是瞄的不准
我们训练一个模型的最终目的,是为了让这个模型在测试数据上拟合效果好,也就是Error(test)比较小,但在实际问题中,test data我们是拿不到的,也根本不知道test data的内在规律(如果知道了,还machine learning个啥 ),所以我们通过什么策略来减小Error(test)呢?
分两步:
- 让Error(train)尽可能小
- 让Error(train)尽可能等于Error(test)
三段论,因为A小,而且A=B,这样B就小。那么怎么让Error(train)尽可能小呢?->把模型复杂化,把参数搞得多多的,这个好理解,十元线性回归,肯定error要比二元线性回归低啊。->low bias
然后怎么让Error(train)尽可能等于Error(test)呢?->把模型简单化,把参数搞得少少的。什么叫Error(train)=Error(test)?就是模型没有偏见,对train test一视同仁。那么怎样的模型更容易有这这种一视同仁的特性,换句话说,更有『通用性』,对局部数据不敏感?那就是简单的模型。->low varience
具体到K-fold Cross Validation的场景,其实是很好的理解的。首先看Variance的变化,还是举打靶的例子。假设我把抢瞄准在10环,虽然每一次射击都有偏差,但是这个偏差的方向是随机的,也就是有可能向上,也有可能向下。那么试验次数越多,应该上下的次数越接近,那么我们把所有射击的目标取一个平均值,也应该离中心更加接近。更加微观的分析,模型的预测值与期望产生较大偏差,在模型固定的情况下,原因还是出在数据上,比如说产生了某一些异常点。在最极端情况下,我们假设只有一个点是异常的,如果只训练一个模型,那么这个点会对整个模型带来影响,使得学习出的模型具有很大的variance。但是如果采用k-fold Cross Validation进行训练,只有1个模型会受到这个异常数据的影响,而其余k-1个模型都是正常的。在平均之后,这个异常数据的影响就大大减少了。相比之下,模型的bias是可以直接建模的,只需要保证模型在训练样本上训练误差最小就可以保证bias比较小,而要达到这个目的,就必须是用所有数据一起训练,才能达到模型的最优解。因此,k-fold Cross Validation的目标函数破坏了前面的情形,所以模型的Bias必然要会增大。
- 在回归中, 相对于OLE的无偏估计, 通过引入正则项来引入bias进而减少variance, 这些方法包括lasso(1阶)和ridge(2阶)
在分类中, 最初bias-variance 分类是用在回归中的, 对于0-1分类, 可以找到类似的分解, 而对于概率分类问题, 预测概率与真实概率的平方误差可以分解成回归的正则形式.
- (Generalized) linear models can be regularized to decrease their variance at the cost of increasing their bias.[10]
- In artificial neural networks, the variance increases and the bias decreases with the number of hidden units.[1] Like in GLMs, regularization is typically applied.
- In k-nearest neighbor models, a high value of k leads to high bias and low variance (see below).
- In Instance-based learning, regularization can be achieved varying the mixture of prototypes and exemplars.[11]
In decision trees, the depth of the tree determines the variance. Decision trees are commonly pruned to control variance.
One way of resolving the trade-off is to use mixture models and ensemble learning. For example, boosting combines many “weak” (high bias) models in an ensemble that has lower bias than the individual models, while bagging combines “strong” learners in a way that reduces their variance.
矩阵特征值, 迹的意义
对称矩阵的特征值不会有复数!
注意理解为什么特征方程的为
$$| A -\lambda I|=0$$
因为对于特征方程
$$AV=VD$$
$$(A-\lambda I)X=0$$
如果$A-\lambda I$是满秩的话就只有一个解, 而对于齐次线性方程, 必然有零解, 然后解唯一, 明显需要非0解, 那么$A-\lambda I$就必须为奇异矩阵, 才有非零解, 那么直接求$|A-\lambda I|=0$即可
注意广义特征值问题是
$$AV=\lambda BV$$
那么这里的$\lambda$就是特征值, V是特征向量
用eigs求前xx个特征值.
稀疏矩阵的特征值计算更方便.

$$A=VDV^{-1}$$
一个变换方阵的所有特征向量组成了这个变换矩阵的一组基。所谓基,可以理解为坐标系的轴。我们平常用到的大多是直角坐标系,在线性代数中可以把这个坐标系扭曲、拉伸、旋转,称为基变换。我们可以按需求去设定基,但是基的轴之间必须是线性无关的,也就是保证坐标系的不同轴不要指向同一个方向或可以被别的轴组合而成,否则的话原来的空间就“撑”不起来了。从线性空间的角度看,在一个定义了内积的线性空间里,对一个N阶对称方阵进行特征分解,就是产生了该空间的N个标准正交基,然后把矩阵投影到这N个基上。N个特征向量就是N个标准正交基,而特征值的模则代表矩阵在每个基上的投影长度。特征值越大,说明矩阵在对应的特征向量上的方差越大,功率越大,信息量越多。不过,特征值分解也有很多的局限,比如说变换的矩阵必须是方阵。
在机器学习特征提取中,意思就是最大特征值对应的特征向量方向上包含最多的信息量,如果某几个特征值很小,说明这几个方向信息量很小,可以用来降维,也就是删除小特征值对应方向的数据,只保留大特征值方向对应的数据,这样做以后数据量减小,但有用信息量变化不大,PCA降维就是基于这种思路。
Matlab中通过eig函数就可求得特征值和特征向量矩阵。
eigs求前几个
对于奇异值分解(用来对任意矩阵进行分解),

一个矩阵的迹等于特征值之和。
特征值在几何上代表的是拉伸系数
迹是特征值之和, 秩是特征值之积
特征值方程$det(A-{\lambda}I)=0$
矩阵对角化, 从而简化矩阵幂的计算!
如何理解特征值和特征向量?
- 我是从线性变换上理解的, 如果在一个线性空间V中有一组基, 这组基的基向量如果都是这个矩阵的特征向量, 那么这个矩阵在这组基下的矩阵就是对角矩阵, 这个对角矩阵的对角元素就是特征值, 每一个特征值代表的就是在相应特征向量上的伸缩系数.
举例子旋转矩阵
首先从长度上看, 不改变任何向量的长度, 所以特征值的模肯定是1, 然后会改变任何向量的方向, 所以这个矩阵没有实的特征向量

如何理解正定矩阵
从定义上来看, 正定矩阵的定义为“正定二次型的矩阵称为正定矩阵”, 正定矩阵的二次型是大于0的, 这个性质在计算上非常有用.
- 对于优化问题中, 一个局部最小点的二阶充分条件就是这个点处的梯度等于0并且黑塞矩阵是正定的. 这样能够保证对任意一个方向d, x+d的函数值都是大于x的. 具体证明就是对x+d进行二阶泰勒展开, 应为梯度是等于0的, 所以x+d的函数值等于f(x)+d的二次型/2. 所以必然大于0 ,所以f(x+d) > f(x), 所以对任意方向d, x+d的函数值都比x要小, 那么x就是极小点.
判定方法就是特征值都大于0, 满秩, 必须对称, 这点是定义上来的, 因为定义是能够正定二次型, 二次型矩阵就是对称的.
进一步理解半正定, 不定.
如何理解线性空间
我的理解就是一个向量的集合, 特点从里面随便取一个或者多个向量进行伸缩变换然后相加减后形成的向量仍然在这个集合里面, 是一个封闭的结构. 然后我们可以从找出相互独立的生成向量, 用他们可以生成集合内所有的向量.
充分条件 必要条件
充分条件就是并联条件

必要条件就是串联条件
Prior, Likelihood, Posterior
MLAPP第3.2节,讲的很好,用了一个叫 number game 的小游戏做例子,通俗易懂
clustering
K Nearest Neighbor 算法 _ 酷壳 – CoolShell
[K-nearest neighbors algorithm – Wikipedia]
(http://en.wikipedia.org/wiki/KNN“)
k-means clustering – Wikipedia
算法杂货铺——k均值聚类(K-means) – T2噬菌体 – 博客园
漫谈 Clustering (1)_ k-means « Free Mind
http://www.codeproject.com/Articles/439890/Text-Documents-Clustering-using-K-Means-Algorithm
因子分析
EM算法
The Expectation Maximization Algorithm
A short tutorial
李航.《统计学习方法》,P155 第9章 EM算法及其推广. 2012.
PCA
隐马尔科夫模型(Hidden Markov Model, HMM)
李航《统计学习方法》第10章 隐马尔科夫模型,讲得非常好,有非常具体的例子
条件随机场(CRF, Conditional Random Field)
introduction-to-conditional-random-fields
李航.《统计学习方法》,P192 第11章 条件随机场. 2012.
LDA
LDA数学八卦
正太分布的前世今生
http://www.tuicool.com/articles/reaIra6
梯度下降-普通, 随机, 改进
普通梯度下降
这里的error和h是向量,m、n分别是样本数量、样本维数
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn) #convert to NumPy matrix
labelMat = mat(classLabels).transpose() #convert to NumPy matrix
m,n = shape(dataMatrix)
alpha = 0.001
maxCycles = 500
weights = ones((n,1))
for k in range(maxCycles): #heavy on matrix operations
h = sigmoid(dataMatrix*weights) #matrix mult
error = (labelMat - h) #vector subtraction
weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
return weights</span>
随机梯度下降
这里的error和h是数值,m、n分别是样本数量、样本维数
def stocGradAscent0(dataMatrix, classLabels):
m,n = shape(dataMatrix)
alpha = 0.01
weights = ones(n) #initialize to all ones
for i in range(m):
h = sigmoid(sum(dataMatrix[i]*weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
return weights</span>
改进的随机梯度下降
m、n分别是样本数量、样本维数
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m,n = shape(dataMatrix)
weights = ones(n) #initialize to all ones
for j in range(numIter):
dataIndex = range(m)
for i in range(m):
alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not
randIndex = int(random.uniform(0,len(dataIndex)))#随机选取样本
h = sigmoid(sum(dataMatrix[randIndex]*weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
del(dataIndex[randIndex])#删除所选的样本
return weights</span>
ensemble learning
http://mlwave.com/kaggle-ensembling-guide/
cvxopt
Portfolio Optimization in Python
http://wellecks.wordpress.com/2014/03/23/portfolio-optimization-with-python/
贝叶斯公式
https://www.52ml.net/20977.html
凸集, 凸函数, 超平面, 优化问题, 真锥和分割超平面, 基本概念
https://www.52ml.net/20968.html
凸集, 直观的理解就是任意两个点形成的线段也在集合内
凸函数.
判定有一阶判定和二阶判定, 用二阶hess判定为其海森矩阵为半正定(严格凸则是正定的)
由梯度求hess矩阵的方法是, 先对梯度转置, 在求梯度.
次梯度算法
proximal GD
对偶问题
利用到拉格朗日函数
对于有约束优化, 局部极小点需要满足KKT条件, 这是一阶必要条件, 二阶条件是拉格朗日函数对x的二阶导数为半正定的(充分条件是正定的)
对于凸函数, 主要满足kkt就是全局最优解
有约束优化, 一般讨论凸优化, 最简单的凸优化问题就是线性规划和凸二次规划(最简单的非线性优化问题), 其中
KKT条件
三个部分
- 正常约束
- 梯度约束
- 不等式约束与相乘为0约束
一般只讨论后两个, 第一个是约束, 后面两个用来求解满足KKT条件的点.
matlab
注意使用的两种结构是
矩阵和cell, cell(dims)创建cell.
读取文件的时候使用imread(sprintf(“image%d”,i)), 这种结构可以进行文件名生成. (sprintf的使用)
save(name, target)
max min 返回 [num, ind]
没有重载
fprintf输出到命令行


SVM
$\frac{1}{2}||w||^2$求导就是$w$, 注意这里是多元函数, 所以有这个结果.
引入核技巧的原因就是, 原来的支持向量机只能应用到线性分类问题, 即使存在噪声数据造成线性不可分, 我们可以引入软间隔来处理. 要想应用到非线性分类中, 我们就要引入核技巧, 想法就是把原来输入空间的数据通过一个非线性映射到特征空间, 使得原来输入空间的超曲面模型就对应于特征空间的超平面模型. 这样我们就可以直接在特征空间学习一个线性支持向量机, 间接学习出一个非线性分类模型.
具体做法是在把线性支持向量机对偶问题的目标函数的内积转而用核函数来求.
含义, 强对偶条件, 为什么对偶问题的解等于原问题的解, 因为SVM的原问题是一个凸二次规划, 然后SVM的前提条件就是数据线性可分, 也就是满足slater条件, 有了这两个条件就满足了强对偶条件. 那么对偶问题的解救等于原问题的解. 如果数据存在离群值使得不满足slater条件, 我们可以引入松弛变量. 如果本身模型是非线性的, 我们就要引入核技巧, 把数据映射到特征空间里使其满足slater条件, 最终满足这个强对偶条件.
(强对偶成立不一定要凸且slater, 是一个充分条件, 当为凸函数, KKT成为充要条件, 换句话说,如果primal problem是一个凸优化问题,且存在$x˜$和 $(λ˜,ν˜)$ 满足 KKT 条件,那么它们分别是primal problem和dual problem 的极值点并且strong duality成立.) 这里注意逻辑, 先满足slater条件和凸函数使得原问题和对偶问题的解一样, 在由充要条件推得满足KKT条件(求出$\alpha$后用来求$w,b$.
强对偶成立 -> 满足KKT条件(其一个性质, 只要满足强对偶都满足KKT, 不一定要凸或者slater), 分为三个部分.(一般我们对凸优化(目标函数和不等式约束函数是凸函数, 等式约束是仿射函数)使用KKT条件, 其满足
- 约束
- 梯度等于0(因为原问题的极值的梯度是等于0的)
- 约束不等式为0(因为p=d)
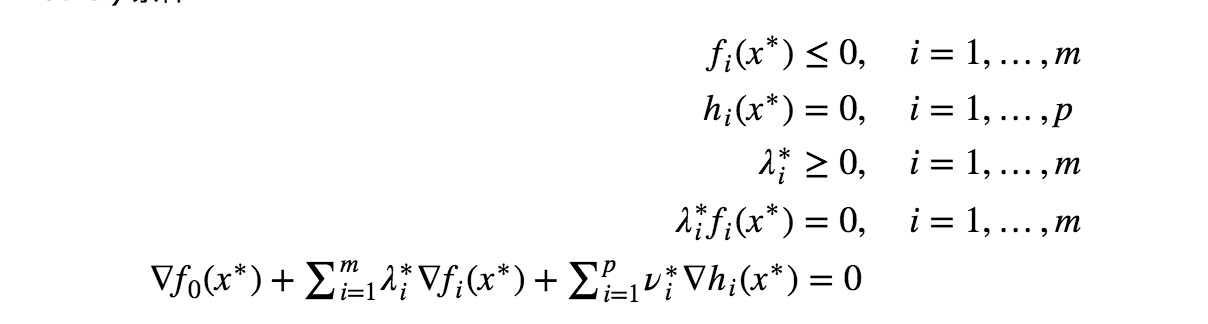
然后剩下的, 就是求解对偶问题了, 由于是凸二次规划问题, 一般用序列最小化算法计算.(这是一种启发式算法)
至于为什么要引入对偶
- 计算方便
- 目标函数表示成内积形式, 就可以引入核技巧, 使得能够处理非线性问题.
总的来说,一个优化问题,通过求出它的 dual problem ,在只有 weak duality 成立的情况下,我们至少可以得到原始问题的一个下界。而如果 strong duality 成立,则可以直接求解 dual problem 来解决原始问题,就如同经典的 SVM 的求解过程一样。有可能 dual problem 比 primal problem 更容易求解,或者 dual problem 有一些优良的结构(例如 SVM 中通过 dual problem 我们可以将问题表示成数据的内积形式从而使得 kernel trick 的应用成为可能)。此外,还有一些情况会同时求解 dual 和 primal problem ,比如在迭代求解的过程中,通过判断 duality gap 的大小,可以得出一个有效的迭代停止条件。
支持向量机的对偶目标函数, 求解需要
- 拉普拉斯算子
- 数据$X$
- target $y$
SMO(序列最小化算法)

http://www.cnblogs.com/coder2012/p/4589963.html
神经网络 kaggle
http://rnavagamuwa.com/open-source/kaggle-grupo-bimbo-neural-network-implementation/
线性模型, 生成模型(GM)与判别模型(DM)
线性模型包括线性回归和logistic回归, 两者前者是学习判别函数, 后者学习条件概率, 进一步, 两者都是判别模型, logistic的判别-生成对是朴素贝叶斯算法(证明用几率logit), 这里朴素贝叶斯是生成方法, 需要先求出联合概率分布, 也就是分别对$f(X)$, $f(Y)$建模, 在求出$f(Y|X)$, 由于$f(X)$的模型不好建, 所以需要很naive的假设, 当然, 线性模型的假设就是需要线性相关, 也是很强的假设.(一般的, 有andrew NG 2001的论文指出DM的误差比GM的误差更小些, 但是GM的收敛速度更快, 也就是在短时间内, GM能更快收敛到最小误差, 相对DM也就更好些), 这是由于GM在求出条件概率时, 先求联合概率分布, 有一个中间步骤.
朴素贝叶斯和logistic最大差别在假设上
GM的独立性假设很强, 比如,在自然语言处理中分析句子的语法树的时候,为了提高性能通常会使用一些冗余度和相关性非常高的特征,这个时候如果使用独立性假设很强的$GM$来处理,效果就不好,但如果不做很强的独立性假设,模型的复杂度又会指数级别增长,很快就无法处理了。不过用对等的 DM Conditional Random Field 来做的话,就可以不用 care 特征之间的关联与否,而有效地利用 rich feature set。(特征丰富模型使用朴素贝叶斯)
隐马尔科夫模型和线性条件随机场也是一对, 前者GM, 后者DM.
朴素贝叶斯
对于朴素贝叶斯, 也就是分类问题, 存在precision(精度), recall(召回)
In simple terms, high precision means that an algorithm returned substantially more relevant results than irrelevant ones, while high recall means that an algorithm returned most of the relevant results.
- precision 和 recall 之间是一个 trade-off ,对于垃圾邮件分类来说,将正常邮件标记为垃圾邮件和将垃圾邮件认为是正常邮件相比,前者是严重得多的错误,所以一般会倾向于调高 precision 。(风险贝叶斯)
- spammer 在不断地进化,针对 anti-spam 工具设计新的 spam 。
一般机器学习算法在处理文本文档的时候多用 Vector Space Model (VSM) 来把一个文档转化为一个定长的向量进行处理。VSM 需要先构建一个词典,用$f^1,…,f^m$表示词典中的m个单词(这里f是 feature 的缩写),我们用$x_1,…,x_n$表示n个训练数据(文档)。
VSM将每个文档转化为一个$m$维的向量,每个维度对应一个单词(feature)。最简单的 VSM 只判断单词是否在文档中出现,例如,我们用$f^j(x_i)$表示文档$x_i$所对应的向量的第$j$维,(除了单词可以作为特征, 发信人也可以作为特征), 那么
朴素贝叶斯学习$P(Y)$和$P(X|Y)$, 进而求出联合分布
$$P(Y,X)=P(Y)*P(X|Y)$$
进一步利用贝叶斯公式
$$P(Y=1|X=x) = \frac{P(Y=1,X)}{P(X)}$$
$$P(Y=0|X=x) = \frac{P(Y=0,X)}{P(X)}$$
首先需要求出$P(Y)$, Y只去0,1,直接利用伯努利分布, 只有一个参数$p=P(Y=1)$.
In probability theory and statistics, the Bernoulli distribution, named after Swiss scientist Jacob Bernoulli,is the probability distribution of a random variable which takes the value 1 with success probability of p and the value 0 with failure probability of $q=1-p$. It can be used to represent a coin toss where 1 and 0 would represent “head” and “tail” (or vice versa), respectively. In particular, unfair coins would have $ p\neq 0.5$.
The Bernoulli distribution is simply $B(1,p)$, 其中$B$是二项分布.
然后是$P(X|Y)$, 分为两个模型, 分别是$P(X|Y=0)$, $P(X|Y=1)$, 进一步又是关于特征的联合概率分布
$$P(X|Y=0)=P(f^1=f^1(X),…,f^m=f^m(X))$$
利用原来的数据, 由于m一般比较大, 这么多特征的联合概率分布建模和处理很麻烦, 所以就做了一个naive的假设, 假设各特征是相互独立的(更准确的说, 相对Y条件是独立的), 那么联合概率分布就可以写成每一个特征各自的概率的乘积.
$$p_0(X)=\prod_{j=1}^mp_0(f^j=f^j(X))$$
其中$p_0(X)=P(X|Y=0)$
如此一来,对联合概率建模就相当于对每一个特征建模, 0-1用伯努利, 连续用高斯等.
logistic 回归的intuition
定义一个几率, 其几率就是一个线性模型.
$$log(\frac{P(Y=0|X)}{P(Y=1|X)})={\beta}^0+\sum_{i=1}^{n}{\beta}^if^i(X)$$
HMM 隐马尔科夫模型
Hidden Markov Model (HMM) 是一个特殊的具有简单线性结构的概率图模型,具有非常简单高效的 inference 和 model fitting (learning) 算法,与此同时,虽然 HMM 中的 Markov 假设,也就是认为时刻的状态在给定 时刻的状态的情况下和更早的状态是 independent 的假设,虽然通常认为过于理想化,但是在实际中通常表现优良,而引入高阶依赖关系之后时常问题的计算和存储复杂度都会变得难以接受,所以 HMM 多年依赖在各种领域中得到了非常广泛的应用。

我们更关注状态序列, 得到一个观察序列, 我们就有了HMM可以解决的三个问题,
主要有三个任务
- Scoring: Forward-Backward 算法,是 Graphical Model 里的 Sum-Product 算法的特例。
- Matching: Viterbi 算法,是 Graphical Model 里的 Max-Product 算法的特例。
- Training: Baum-Welch 算法,是 EM 算法的特例。
更深一层的理解, 其实是先得到每一个时刻状态的条件概率, 全部相加起来, 利用边缘分布, 求出scoring ,也就是观察序列的概率的.
scoring推断出任意状态条件概率->(离散相加得边缘分布, 连续积分得边缘分布)观察序列概率(前后向算法, 利用markov条件, 就是条件独立性, 包含两个内容, 一个是状态独立, 一个观察独立), 前向算法, 本质上是求联合概率密度(条件独立性展开(这里求得是一个与概率正相关的量), 前向算法只能求出某位状态的条件概率, 而后向算法可以求出中间状态的条件概率(相当于引入了新的数据). 这样正相反相遍历一遍然后求和就可以求出边缘分布也就是观察序列的scoring.
matching推断出状态序列
training得到模型参数.
前两者属于inference, 就是推断问题, 推断结果, scoring推断观察序列真假, matching推断观察序列下面的状态, training学习模型参数
HMM模型又三个参数$\pi,A,B$, 其中$\pi$是初始状态分布, $A$是状态转移矩阵, $B$是, 这里包含条件独立性, t+1时候的状态只与$t$时候的状态有关,每个时刻的观察值只与当前状态有关, 与之前的状态无关, 称为马克洛夫条件, 所以称为马克洛夫模型.
图模型.(更清楚得看到各随机变量的条件独立性)
高斯分布
积分是一件很困难的事情,就算是装备了 Wolfram Mathematica 的 PhD 也不能随便夸海口的,因为有很多积分式本来就没有一个式子可以把结果写下来。当然你可以像gamma函数那样自己定义新的符号来隐藏后面算不出来的一大坨式子,不过这对于最终需要做数值计算来说好像是躲得了和尚躲不了庙啊。所以我们就不说这些歪门邪道了,正统的解决方法主要有两种。
第一种是把概率分布限制到高斯分布上,由于高斯分布像开了外挂似得,求 marginalization 和 conditioning 之后都还是高斯分布,并且本身只需要用均值和方差两“个”量即可描述,所以我们在这里碰到的积分问题都可以解析地计算出来,这里介绍一种代表性的算法叫做 Kalman Filtering
另外一种方法是放弃精确计算,采用近似计算的方法,这里也介绍一种代表性方法叫做 Particle Filtering。
高斯分布有几个很好的性质:
- 一个服从多维联合高斯分布的随机变量$X$的线性投影$AX$仍然服从高斯分布
- 一个服从多维联合高斯分布的随机变量$X$在对其中一部分维度进行 marginalization 和 conditioning 的时候,结果仍然是多维联合高斯分布
我们回顾一下上次推导得到的 Forward-Backward 算法里关于${\alpha}$与${\beta}$的递推式
$${\alpha}(z_{t+1})={\int}_{z_{t}}{\alpha}(z_t)p(z_{t+1}|z_{t})dztp(x\{t+1}|z_{t+1})$$
$${\beta}(z_t)=\int_{z_{t+1}}p(x_{t+1}|z_{t+1}){\beta}(z_{t+1})p(z_{t+1}|z_t)dz_{t+1}$$
这里积分的计算可以利用概率假设为高斯分布来计算.
其中$A$的转移分布可以看做高斯分布.有
$$p(x_t|z_t)=pdf(N(z_t,\sum))$$
其中$\sum$是协方差.
对于状态转移, 我们先假设初始状态$z$是高斯分布, 那么线性映射$f(z_{t})=Az_{t}$也满足高斯分布.高绿一个误差$f(z_{t})=Az_{t}+\epsilon$, 其中$\epsilon$也满足高斯分布,有
$$p(z_{t+1}|z_{t})=pdf(N(Az_{t},\sum))$$
缺陷是限制了状态转移只能是线性映射.所以卡尔曼滤波为线性方法, 这点缺陷非常大, 所以引入extended卡尔曼滤波(扩展), 将非线性状态转移线性化近似.
总的来说就是当假设$B$观察序列概率分布服从正态分布, 同时$\pi$初始状态服从正太分布, 状态转移为线性映射, 那么$A$状态转移条件概率就可以写成正太分布.(双正太分布的条件概率分布也服从正太分布, 其实就是条件分布, 联合概率分布为正太分布,那么他的条件分布和边缘分布都服从正太分布)
谱聚类
矩阵也有矩阵的谱,矩阵的谱就是矩阵特征值的概念,是矩阵所固有的特性,所有的特征值形成了矩阵的一个频谱,每个特征值是矩阵的一个“谐振频点”。
总的来说, 是应用了LE降维(非PCA降维, LE降维需要先构造相似度矩阵, 分解后直接得到每个点降维后的数据, 但是PCA降维需要进一步进行映射, 一个是对相似度矩阵, 一个是对数据集)
laplacian矩阵

思路上的话,大致就是你要确定好你的目标(想要得到什么样的分割),然后得到一个目标函数,然后尝试把这个目标函数(一般是离散优化没法解)relax 为特征值问题阿之类的来进行近似, 和kmeans一样需要指定类别, 不需要指定的就是也可以试试不需要指定类别数目的算法,比如 Mean Shift,Affinity Propagation(标签传播) 之类的。
如果按照简正运动模式的想法来分析,做K-means之前还应该对各个特征矢量按其本征值进行加权,乘以eigenvalue^(-0.5),因为前面的维度的区分性要高于后面的维度(这段日后分析?)
如果用 Laplacian Matrix 就是取小特征值,如果用 similarity matrix 就是取最大的。(相似矩阵和拉普拉斯矩阵是相反的关系), 总的来说拉普拉斯图用的是相似度矩阵,PCA用的是协方差矩阵.一般 k 类聚类实际上是取了 k-1 个特征向量,因为丢掉了 constant 的那个。但是也有些描述是没有专门去丢掉那个的,就是留在那里也没有什么影响,反正是 constant 的。
相似度, 欧式, 余弦, 皮尔逊相似度, 高斯核.我见过的一般主要就是三种:1. 全连通 Gaussian decay;2. k 近邻图(互K近部图);3. ε-近邻图。
正确性 : 有 ground truth 的话,可以用 accuracy 或者 mutual information 之类的来衡量,需要先把聚类的类别做一个映射到正确的类别上。
$$L=D-W$$
其中$D$为度矩阵, $W$为邻接矩阵.
性质如下
- 半正定矩阵
- 最小的特征值是0, 相应的特征向量是全1向量, 证明让其乘以这个向量等于0.
- 对于任何一个向量$\in R^n$
有$$f’Lf=\frac{1}{2}\sum_{i,j=1}^{N}w_{ij}(f_i-f_j)^2$$
谱聚类就是把样本构成一张图, 然后进行图分割形成很多个子图, 使得不同子图内的权重尽可能小, 相同子图的权重尽可能大.
图分割方法有很多
- 比例割(ratio cut)
- 归一割(normalized cut)
- 不基于图, 用SVD
最常用的相似度度量就是高斯核函数.
目标函数, 一般采用使得割掉的边的权值和最小(这样使得联系不大的节点被割开), 也就是cut值(cut值就是这个子图被割掉的边权重之和)最小. 但是直接使用就有可能使得每个类的大小不合理, 比如两类问题, 直接割最小的一个变, 那么一个类只有一个点了, 显然不合理, 所以引入比例割, 把每一个子图的cut值除以其节点数(那么节点数越大, 值就越小了).
那么对于ratiocut, 其值与拉普拉斯矩阵的二次型$f’Lf$是一致的.
根据特征值的定义
$$Lf=\lambda f$$
两边做成$f’$
$$f’Lf=\lambda f’f=\lambda n$$
说明了拉普拉斯矩阵对特征向量的二次型是一个常数, 也就是节点数乘以特征值. 那么我们最小化这个二次型就相当于找到$L$最小的特征值和其对应的特征向量就可以了. $L$有一个性质是最小的特征值是0, 特征向量是1, 不满足垂直1的条件. 根据Rayleigh商条件, 我们取第二小的特征值和特征向量.
对于特征向量$v$, 是连续的实数, 我们需要转换成对应的离散值, 简单的直接根据正负划分, 复杂点可以用k均值聚为两类. 进一步推广, k分类, 我们取前k个最小的. 在按行进行聚类.
latex
常用公式





系数矩阵存储
COO:Coordinate Format COO格式使用行下标、列下标和数据值三元组来表示每个非零元素,所以总共需要保存非零元素个数的三倍个值
CSR:Compressed Sparse Row CSR格式的列下标向量和数据值向量与COO格式类似,在行下标表示上做了压缩。根据数据的排列规则,只需要指定在哪个数据换到下一行就行。
CSC:Compressed Sparse Column CSC格式的行下标和数据值向量与COO格式类似,在列下标上做了压缩。根据数据的排列规则,只需要指定在哪个数据换到下一列就行。
julia中使用csc存储, 压缩列, 直观的,对于列指针, 取一阶差分, 就可以得到每一列的非0元素个数
sprand(5,5,0.1)
其中0.1是非零元素生成几率.
概率论
生男生女问题
两种题干
- 一种是已知一个, 在生(独立事件)
- 一种是已知两个, 再用条件概率公式.
概率和统计的区别?
概率是知道模型推出结果
统计是知道结果归纳出模型和规则
现代数学最重要的是分解(特征分解), 变换(线性变换), 逼近(一致性定理, 如
一般在概率论, 线性代数, 泛函分析
复杂系统分析 -> 图模型(统计学习), 复杂网络
分析过程
- 描述底层运动
- 建立普适的表达
- 微观与宏观的变换的联系
集合论
在集合的基础上, 现代数学有两大家族: 分析(极限, 函数)和代数(线代, 泛函(一般的线性空间)
我们学的黎曼积分(无限分割区间, 取矩阵面积和的极限)
现代概率和几何(微分集合, 流形)都建立在分析或者代数的基础上
最基本的概念是, 集合, 关系, 函数, 等价.
BLAS(数值矩阵运算的库, 基础线性代数子程序, 理解为函数接口, 不同的库可以由不同的实现, 甚至提供更复杂的功能, ) -> lapack(提供矩阵分解, 最小二乘法等)
计算思维

图灵完备, 拥有数字, 赋值, 输入输出, 循环和比较, 可以解决计算能解决的所有问题.
对于计算思维. 我的理解是
- 演绎信息来解决问题的思维, 比如我们描述了x*x=y这个过程, 怎么求出y的平方根, 需要给出一由y演绎出x的过程.
- 抽象的思维, 抽象的最终目的是模块化(封装, 接口)
抽象包含过程抽象和数据抽象.
- 其中过程抽象就是从计算过程中抽象出普适的东西, 比如优化算法中, 虽然有很多算法.
- 数据抽象, 就是面向对象这种思维, 把一个数据类型和对他的操作进行抽象, 继而抽象出接口来使得各个抽象类型相互隔离, 增大模块化能力.
计算过程包含确定过程和随机过程
确定的输入产生不确定的结果, 就是随机的计算过程, 进一步引出随机游动, 更进一步蒙特卡洛, 构建模拟模型更简单, 可以把一系列微分方程组转换成等价的随机过程. 有一句话是, 模拟的结果都是错误的, 但是其中一些是有用的, 求出近似的结果
在具体解决一个问题的时候, 可以把他转化成已经解决的问题, 大部分问题都可以转换成背包问题(动态规划)和图优化问题.
进一步用机器学习来用计算机挖掘隐藏的模型.
复数
旋转90度, 数的新维度.
为什么引入无理数?
这与一个集合的封闭性有关.
因为有理数在指数运算下不是封闭的, 会引出无理数和虚数, 只在加减乘除下封闭.
动态规划和分治
动态规划有重复子问题和最优子结构
动态规划的子问题和原问题相差不大(斐波那契数列), 但是分治相差很大(快排).
感知器算法
感知器算法是支持向量机和神经网络的基础, 其基于数据线性可分.
有两种形式, 原问题形式和对偶形式, 和支持向量机是对应的, 对偶计算时利用拉格朗日算子.
利用对偶形式时, 引入内积, 同时把参数转换成拉格朗日算子, 训练时需要原来的数据之间的内积, 所以提前算出Gram矩阵打表加快速度.
对偶形式模型为
$$f(x)=sign({\sum}_{j=1}^{N}{\alpha}_jy_j(x_j*x)+b)$$
训练规则是选出$f(x)*y\leq0$的点, 对拉格朗日算子进行迭代
$${\alpha}_i\leftarrow{\alpha}_i+\eta$$
$$b\leftarrow{b}+{\eta}y_i$$
此算法是基于随机梯度下降, 一次选一个错误分类点, 并非一次全部.
线性可分时收敛, 但是解有无穷个, 不保证每次解一样.
knn
knn没有模型参数, 包含三个要素:
- 距离度量(一般使用欧式距离,更一般的使用$L_p$距离)
- k值选择(k越大, 模型越简单)
- 分类决策规则(一般选比例最高, 即经验风险最小)
但是要计算距离向量, 为加快速度构建KD树, 平均复杂度是$logN$, 此为经验风险最小(多数表决), 但是朴素贝叶斯是期望风险最小
期望风险, 经验风险和结构风险
模型的假设空间, 可以是条件概率的集合, 或者决策函数的集合.
这两个集合分别又各自的模型参数决定的函数族或者条件概率分布族. 由此有两种模型, 一种概率模型, 一种非概率模型.
首先是损失函数和风险函数的概念, 风险函数中包含损失函数.
损失函数常用的有四种, 对于非条件概率分布模型有三种, 条件概率分布为对数损失函数
- 0-1误差损失
- 平方损失函数
- 绝对损失函数
- 对数损失函数$L(Y,P(Y|X))=-log(f(Y|X))$
当回归采用平方损失的时候, 可以用最小二乘法进行解析求解.
- 期望风险是关于联合分布的期望损失.
经验风险是关于样本集的平均损失.(根据大数定理, 当$N\rightarrow\infty$时, 经验风险趋于期望风险, 一般像用经验风险代替期望风险, 但是样本有限, 所以对经验风险进行一定的矫正. 进一步就有了策略, 经验风险最小和结构风险最小.
经验风险最小认为经验风险最小的模型是最好的模型, 代表是极大似然估计(当模型是条件概率分布, 损失函数是对数损失函数, 就是极大似然估计), 为了防止过拟合(样本数目少), 引入正则化项(关于复杂度, 一般用$f(w)$表示), 常用的有L1,L2.
- 结构风险小对样本集比较少和对测试数据有较好的预测, 使得模型复杂度和经验风险同时小, 如贝叶斯估计中的最大后验概率估计(当模型是条件概率分布, 损失函数是对数损失函数, 复杂度用模型的先验概率表示, 结构风险最小等于最大后验概率估计)
k-fold交叉验证
相当于不停的进行简单交叉验证, 最后进行多数表决
泛化误差上界公式
一般我们关心的不是经验风险, 而是期望风险(数据太少求不出来), 其代表泛化能力, 对任意一个函数, 至少以概率$1-\delta$有不等式成立. d是假设空间函数的个数(所以越简单, 样本越多, 泛化误差上界越低).
$$R(f){\leq}\hat{R}+\epsilon(d,N,\delta)$$
其中$$\epsilon=\sqrt{\frac{1}{2N}(logd+log\frac{1}{\delta})}$$
不等式左边为泛化误差, 右边为泛化误差上界. 这说明期望风险存在上界, 其关于经验风险和一个关于N和logd的函数,
ML模型综述

可以看到各个模型相互推导.
内积, 外积
假设$x$是列向量.
$xx^T$是外积
$x^Tx$是内积
LDA和QDA
注意LDA的假设是各类下协方差相同, 但是如果不相同的话, 就会有问题, 就比如ANOVA模型假设各类方差一样. QDA就没有相同协方差假设. 当然LDA可以对每一个类计算协方差矩阵, 但是仍然有问题
If you have the heterogeneity (as detected for example by Box’s M test) and you don’t have QDA at hand, you may still use LDA in the regime of using individual covariance matrices (rather than the pooled matrix) of the discriminants at classification. This partly solves the problem, though less effectively than in QDA, because - as just pointed - these are the matrices between the discriminants and not between the original variables (which matrices differed).
这里LDA实际上包含高斯判别分析和fishers 判别分析, 其中fishers的只针对两个类, GDA是假设各条件概率都是多变量高斯分布.
QDA
高斯贝叶斯分类器
生成模型都是贝叶斯分类器, 根据一些特性的不同, 分为很多种方法, 线性判别分析和二次判别分析就是在高斯分布假设的情况下, 各类的协方差相同和不同的区别, 本质都是高斯分布贝叶斯分类器. 对其他的概率密度, 实际上都可以转换成高斯分布, 利用GMM模型来表达即可, 可以模拟任何分布.
一般的判别分析都是贝叶斯分类器, 只不过是高斯分布分类器, 根据协方差和先验概率的不同, 可以分为3种情况.
$\sum_i=\sigma^2I, P(w_i)= \frac{1}{c}$
这时实际上就是一个距离分类器当$\sum_i=\sum$
这时候实际上就是线性判别分析
$$g_i(x)=ln[p(x|w_i)p(w_i)]=lnp(x|w_i)+lnp(w_i)$$
为高斯分布
$$g_i(x)=-\frac{1}{2}(x-\mu_i)^T(\sum)^{-1}(x-\mu_i)+lnp(w_i)$$
$$g_i(x)=-\frac{1}{2}x^T(\sum)^{-1}x+\mu_i^T(\sum)^{-1}x-\frac{1}{2}\mu_i^T\mu_i+lnp(w_i)$$
最后可以化为
$$g_i(x)=w_i^Tx+w_{i0}$$
- 标准高斯分布
$$g_i(x)=w^TW_ix+w_i^Tx+w_{i0}$$
实际上就是二次判别分析了, 分类平面为二次曲线.
在高斯判别分析中我们假设各类协方差相同, 实际上就是第二种情况, 这时候就是一个线性判别函数.
- 对特征数比较多的时
使用朴素贝叶斯准则, 降为单变量高斯分布.
一般使用的都是高斯分布朴素贝叶斯, 其他分布不好计算.
需要注意的是非朴素判别分析的协方差矩阵由于存在特征之间的关系, 所以一般协方差矩阵都是奇异矩阵. 改进方向是先用PCA进行特征变换.
条件概率的参数估计
一般分为参数估计和非参数估计.
对于参数估计即给定概率密度函数的形式, 只需要拟合出参数, 一般使用最大似然估计.$L(\theta)$, 表示在参数为$\theta$的情况下, 样本出现的概率, 实际上似然函数就是条件概率.
$$L(\theta)=p(D|\theta)=\prod_{i=1}^np(x_i|\theta)$$, 求对数, 之后对参数求导为0就可以得到结果.
一般如果不是高斯分布, 那么可以由GMM(高斯混合模型)来逼近任意的概率密度函数. 直接对对数似然函数进行求导为0很难得到解析解, 所以一般使用近似方法求解, 最常用的方法就是EM算法.
所以可以看出的是这是非监督算法. 只需给训练集而不用给目标, 训练出GMM模型.
GMM的EM算法可以这样理解, 模型有两组未知量, 首先是模型的参数, 然后是每一个样本出自哪一个高斯分布, 当两组都未知, 但是我们由一组可以推出另外一组的时候, 我们就可以利用迭代的过程, 首先由初始参数计算样本出自任一高斯分布的概率, 然后用这个概率反过来求模型参数, 改迭代过程和k-means一样.
GMM为混合密度函数.
把GMM应用搞贝叶斯分类器, 需要对每一个样本训练一个GMM..
对于EM算法, 为什么能收敛? 即使能收敛, 为什么能保证收敛于似然函数的极值?
当存在隐含数据(参数), 比如GMM的哪一个高斯分布.
对于似然函数$L(\theta)=\sum lg p(D|\theta)=\sum lgp(X,Y|\theta)$
由于$Y$未知, 直接对Y求期望
$$E_Y[L(\theta)]=\int lnp(X,Y|\theta)p(Y)dY$$
此时只有$\theta$是未知的了, 原来的隐变量已经被消去了, 对其进行优化就行了, 但是这里要求$P(Y)$, 这是非常困难的事情, 所以EM的做法是先设置$\theta$的一个猜想值, 然后在已知$X,\theta$的情况下估计$p(Y|\theta,X)$, 然后用这个条件概率代替$P(Y)$,即
- E步: $$Q(\theta;\theta^g)=\int lnp(X,Y|\theta)p(Y|\theta^g,X)dY$$
- M步: $$\theta^*=(argmax)_\theta Q(\theta;\theta^g)$$
注意这里$\theta^*$并不是对数似然函数的极值点, 只是一个对原来的猜想改进的值.
有证明$Q(\theta,\theta^{t+1})\geq Q(\theta,\theta^{t})$, 因此算法是收敛的, 能收敛到极大值, 但是不能保证收敛到最大值.(与初始值有关), 因此最好使用一些先验只是来对初始值进行设定, 当缺少先验知识的时候, 可以多试几个初始点, 根据结果选最优的.
为什么要取对数
因为当特征维数过大的时候, 样本的概率密度值很小, 可能超出计算机表示的精度范围, 造成计算的不稳定性.
最大似然估计和贝叶斯估计
两者最大的区别在于, 最大似然估计认为$\theta$就是一个常数, 找到似然函数最大的$\theta$, 我们就认为$\theta$的值不变了, 但是贝叶斯认为$\theta$是一个随机变量, 而不是一个固定的取值.
一个过程是先用样本集估计出最优的参数, 然后根据参数求出条件概率密度$p(x|\theta^*)$, 而贝叶斯估计是根据样本集先估计参数的条件概率分布, 但是利用这个计算$P(x|D)$
$$p(x|D)=\int p(x,\theta|D)d\theta=\int p(x|D)p(\theta|D)d\theta$$
当样本数目趋向于无穷大的时候, 最大似然估计和贝叶斯估计的结果就是一样的了, 也就不存在不确定性了.
贝叶斯估计的优点是在有限样本的情况下, 性能更好.
共轭先验分布
当$p(\theta)$和$p(\theta|D)$属于同一分布族, 那么就称为共轭先验分布.
k-means
k-medoids算法
基于不同的相似度
距离函数, 当每个团呈圆形分布的时候适合采用欧式距离进行分类, 但是当团的形状为椭圆的时候, 适合采用明氏距离(用来度量样本与一个团的距离)这里可以看成高斯分布$e$的指数, $\Sigma$可以看成样本的分布.
降维
主要有两种方法, 一种是PCA, 一种是基于fisher准则的(保留可分性, 主要利用了瑞利商问题)
注意两个常见的导数
$$\frac{w^T\sum w}{dw}=2\sum w$$
$$||w||^2=w^Tw$$
$$\frac{||w||^2}{dw}=\frac{w^Tw}{dw}=2w$$
PCA的损失函数是
$$J(e_1,…,e_i)=\sum_{i=d’+1}^d e_i^T{\sum}e_i=\sum_{i=d’+1}^d\lambda_ie_i^Te_i=\sum_{i=d’+1}^d\lambda_i$$
这里解有无穷个, 因此约束$||e_i||2=1$
$$J(e_1,…,e_i,\lambda_1,…,\lambda_i)=\sum_{i=d’+1}^de_i^T\sum e_i-\sum_{i=d’+1}^d\lambda_i(e_i^Te_i-1)$$
有
$$\frac{J(e_1,…,e_i,\lambda_1,…,\lambda_i)}{de_j}=\sum e_j-2\lambda_je_j=0$$
所以有
$$\sum e_j=\lambda_ie_j$$
即求协方差矩阵的特征值.
其中协方差矩阵求法为
$$\sum=\frac{1}{n}\sum_{i=1}^{n}(x_i-\mu)(x_i-\mu)^T$$
对于fisher准则
$$max_wJ(w)=\frac{w^TS_bw}{w^TS_ww}$$.
这里的J(w)就是fisher准则函数.
这个函数的最优值由广义特征值和特征向量给出.$eig(S_b,S_w)$, 即$S_w^{-1}
S_b$的特征值.
证明方法是利用对偶原理, 因为本身解是无穷个, 当$w^$是一个解得时候, $\alpha w^ $也是一个解, 那么固定一下参数, 令分母为一个常数$C$, 有
$$J(w)=w^TS_bw$$
$$st. w^TS_ww=C$$
利用对偶原理
$$J(w,\lambda)=w^TS_bw-\lambda w^TS_ww$$
对$w$求导
$$\frac{J(w)}{dw}=2S_bw-2\lambda S_ww=0 $$
有
$$S_bw=\lambda S_ww$$
这就成了一个广义特征值求解问题. 如果$S_w$可逆, 直接求$S_w^{-1}S_b$的特征值就行了.
那么对于fisher判别分析, 我们求出$S_b,S_w$后, 求广义特征值即可, (这里利用了类别信息), 但是PCA没有利用类别信息, 属于无监督的方法, 直接对原始数据进行了压缩求解.
PCA和LDA
fisher准则是LDA在二维下的降维.
lda是有监督的降维,使得训练数据在新的子空间中类间方差变大,类内方差变小。
pca是无监督降维,使得所有数据(训练+测试)在新的子空间中投影的方差尽量大。
LDA选择分类性能最好的方向,PCA选择样本点投影具有最大方差的方向。
你做的结果差不多,并不能说明lda没有作用,应该是数据本身的分布造成的结果近似。lda更多依赖于数据的均值信息,当两类均值不具备投影后能分开的特性时,lda的性能发挥不出来。
one-hot编码
可以直接用
function one_hot(y)
n = maximun(y)
return eye(n+1)[y,]
end
AUC
MATLAB自带plotroc()方法,绘制ROC曲线,参数如下:
plotroc(targets,outputs);
第一个参数为测试样本的原始标签,第二个参数为分类后得到的标签。
两个为行或列向量,相同维数即可。
AUC matlab代码:
function [result]=AUC(test_targets,output)
%计算AUC值,test_targets为原始样本标签,output为分类器得到的标签
%均为行或列向量
[A,I]=sort(output);
M=0;N=0;
for i=1:length(output)
if(test_targets(i)==1)
M=M+1;
else
N=N+1;
end
end
sigma=0;
for i=M+N:-1:1
if(test_targets(I(i))==1)
sigma=sigma+i;
end
end
result=(sigma-(M+1)*M/2)/(M*N);
多类与0-1分类
一般对于0-1分类的损失函数.
这其实是似然函数.
$$-y_ilog(h(x_i))-(1-y_i)log(1-h(x_i))$$
对数损失是
$$L(y,P(y|x))=-log(P(y|x))$$
那么对于多分类问题, 可以转换成多0-1变量, 之后对每一个变量用似然函数损失就可以了.
bagging 和 boosting
bagging是均匀采样, 因此可以并行操作训练
boosting是根据错误率采样, 错误率高更容易被采到, 因此只能顺序执行.
随机森林包括行采样和列采样, 属于bagging
boostingTree 属于boosting方法, 采用决策树作为弱分类器, 如果采用决策树桩就是最简单的adaptive boosting.
梯度boosting



GBDT
实现如下
class GradientBoosting(object):
"""Super class of GradientBoostingClassifier and GradientBoostinRegressor.
Uses a collection of regression trees that trains on predicting the gradient
of the loss function.
Parameters:
-----------
n_estimators: int
The number of classification trees that are used.
learning_rate: float
The step length that will be taken when following the negative gradient during
training.
min_samples_split: int
The minimum number of samples needed to make a split when building a tree.
min_impurity: float
The minimum impurity required to split the tree further.
max_depth: int
The maximum depth of a tree.
regression: boolean
True or false depending on if we're doing regression or classification.
debug: boolean
True or false depending on if we wish to display the training progress.
"""
def __init__(self, n_estimators, learning_rate, min_samples_split,
min_impurity, max_depth, regression, debug):
self.n_estimators = n_estimators
self.learning_rate = learning_rate
self.min_samples_split = min_samples_split
self.min_impurity = min_impurity
self.max_depth = max_depth
self.init_estimate = None
self.regression = regression
self.debug = debug
self.multipliers = []
# Square loss for regression
# Log loss for classification
self.loss = SquareLoss()
if not self.regression:
self.loss = LogisticLoss()
# Initialize regression trees
self.trees = []
for _ in range(n_estimators):
tree = RegressionTree(
min_samples_split=self.min_samples_split,
min_impurity=min_impurity,
max_depth=self.max_depth)
self.trees.append(tree)
def fit(self, X, y):
y_pred = np.full(np.shape(y), np.mean(y, axis=0))
print (y_pred)
for i, tree in enumerate(self.trees):
gradient = self.loss.gradient(y, y_pred)
tree.fit(X, gradient)
update = tree.predict(X)
# Update y prediction
y_pred -= np.multiply(self.learning_rate, update)
if self.debug:
progress = 100 * (i / self.n_estimators)
print ("Progress: %.2f%%" % progress)
def predict(self, X):
y_pred = np.array([])
# Make predictions
for i, tree in enumerate(self.trees):
update = tree.predict(X)
update = np.multiply(self.learning_rate, update)
# prediction = np.array(prediction).reshape(np.shape(y_pred))
y_pred = -update if not y_pred.any() else y_pred - update
if not self.regression:
# Turn into probability distribution
print (y_pred)
y_pred = np.exp(y_pred) / np.expand_dims(np.sum(np.exp(y_pred), axis=1), axis=1)
# Set label to the value that maximizes probability
y_pred = np.argmax(y_pred, axis=1)
return y_pred
树方法的一个总结
一般分为三种树, 分类树, 回归树, xgboost树, 三者总体是相同的, 不同的地方有
- 分裂后计算信息增益的方式不同, 分类树用熵减, 回归树用方差减, boost用梯度信息, xgboost更进一步则用了二阶导数信息.
logistic 损失的梯度和hessian矩阵
loglossobj <- function(preds, dtrain) {
# dtrain is the internal format of the training data
# We extract the labels from the training data
labels <- getinfo(dtrain, "label")
# We compute the 1st and 2nd gradient, as grad and hess
preds <- 1/(1 + exp(-preds))
grad <- preds - labels
hess <- preds * (1 - preds)
# Return the result as a list
return(list(grad = grad, hess = hess))
}
机器学习问题
不用说这部分是机器学习面试的重点。面试中遇到的机器学习算法主要有线性回归、朴素贝叶斯、决策树、GDBT、随机森林、Adaboost、逻辑回归(和Softmax)、SVM、神经网络和卷积神经网络。遇到很多次让写逻辑回归的极大似然估计的推导。SVM会问思想,我SVM掌握的太少答的不好。神经网络会问随机梯度下降和反向传播,要写出式子来的。卷积神经网络就遇到过一次,当时不知道后来上网学习了一下挺有意思的。损失函数、过拟合、算法的优缺点是经常问到的点,另外遇到的其他问题有这么几个:机器学习算法中哪些是回归算法哪些是分类的。他们的产品要做用户流失预测须要提取哪些特征的。其他我还遇到过倒排索引、推荐算法之类的问题。
前些天刚刚面了俩家。传统机器学习算法也不难,把李航那本刷完就够用了。SVM对偶问题可能要多看看。python的sklearn对这些传统算法封装好,可以了解一下。
大部分问题应该都跟深度学习无关。
- 标准的理论(VC bound,model selection, overfitting)
- 标准的模型(SVM,Random Forest,Decision Tree,NN)
- 标准的优化算法(MCMC,MLE,EM,SGD)
- 标准的库(TensorFlow,WEKA,Spark)
大部分问题应该都跟深度学习无关。标准的理论(VC bound,model selection, overfitting)标准的模型(SVM,Random Forest,Decision Tree,NN)标准的优化算法(MCMC,MLE,EM,SGD)标准的库(TensorFlow,WEKA,Spark)
问题
- 用过哪些DL的library呀?
- 现在的DL 的state of art model有哪些呀?
- 如果如理diminishing gradient的问题呀?
- 如果同时处理文本文档+图片呀?
- 如果防止overfitting呀?
- 如何pre-train model呀?
- 能否自己在服务器上用distributed computing部署一个现有的model 呀?
这个问题其实很不错,涉及到一个很本质的问题就是卷积为什么能够work - 这个可能的答案可以很多:
- 比如你可以从正则化的角度说这是一个很好地降低参数数量的方法
- 也可以从统计的角度说卷积很好地抓住了local correlation以及spatial invariance
- 也可以从编程的角度说卷积是一个很有效地提高计算效率的方法,表示你对工程很感兴趣
- 也可以从神经科学的角度说local connection是biologically inspired(但是你估计需要讨论一下为什么生物没有卷积这样共享参数的机制)
这几个角度可以很好地考察被试者在深度学习上的侧重点和经验,应该说是个甄别的好题目。
CNN的特点是抓住局部相关性,而且是共性的局部相关性,高层的视野区域增大,如果区域之间的相关性稀疏(比如人脸,不可能眼睛满脸飞),就不适合直接conv了;描述长距离的(稀疏)关系,可以LSTM等。
Large Scale Spectral Clustering with Landmark-Based Representation (in Julia)
光谱聚类, 依靠光谱(也就是特征值分解), 光谱聚类需要相似度矩阵而不是原矩阵来计算.
根据相似度计算的不同, 可以分为很多种光谱聚类, 其中一种就是
$$W=D^{\frac{1}{2}}AD^{\frac{1}{2}}$$
计算出前k个最大的特征向量后, 对特征向量进行k-means聚类.
需要注意的是
- 实对称矩阵的特征值是实数;
- 实对称矩阵的不同对称值对应的特征向量是正交的;
VAE
Variational Autoencoder in Tensorflow – facial expression low dimensional embedding
NP完全问题
线性规划问题
人体检测
Batch Normalization Layer
Implementation of Batch Normalization Layer
CNNs
Classification in Remote Sensing Optical Images by CNNs
Ways for Visualizing Convolutional Networks
GANs
Generative Adversarial Networks
转置卷积
一般卷积层的参数就是五个.
- 输入通道数
- 输出通道数
- 卷积核大小(kernel)
- 步长(stride)
- padding
转置卷积是相对普通卷积而言的, 本质也是一种卷积操作, 在原来卷积的基础上多了很多padding来源, 根据原来的卷积操作, 可以得出相应的转置卷积的参数, 卷积核大小和步长是不变的, 但是padding会变化, 然后根据k,p,s来确定增加的padding.
- 在每个输出之间插入$s-1$的0单元
- 在四周加入$k-p-1$的padding