前言

最近看SICP的时候愈发发现里面的思想和haskell的书籍路线基本很像, 两者都是从抽象开始, 包括

• 函数抽象 -> 递归/lambda/柯里化/高阶函数
• 数据抽象 -> 抽象数据/闭包/构造类型/通用型操作/模式匹配
• 状态处理 -> Monad/IO/流/对象

不同的是haskell在这之外主要讨论了其内部的类型系统, 类型类以对类的进一步抽象(也是一种数据抽象

从最简单的过程/函数/对象开始, 我们通过把这些基本的元素结合在一起, 就能形成非常复杂的结构.

小想法

为了控制我现在博客每篇文章的质量, 以便以后自己也方便查阅(主要是为了避免有时候自己写的代码, 过了些日子在看都不知道怎么想出来的…), 在这里记录一下我的思考.

现在写博客主要的流派有

• 文章数量很大, 事无巨细的…比如如何安装homebrew, 今天遇到了什么BUG, 都当作一篇发出来.
• 虽然文章数量很少, 但是每篇文章都很长的, 这种适合写比较大的笔记和一些思考的过程

既然作为思考的载体, 那么琐碎的东西自然是不需要记录的, 而长文章在写的过程中其实也是一种思考, 人的记忆总是有时效的, 留下的东西自己以后也不一定记得. 但是作为自己思考的结果, 如果能在看一遍, 印象自然比以前更深了, 书读百遍, 而书读的是别人的成果, 自己的成果读起来我觉得可能更适合自己.

所以, 以后记录的每篇博客都会是相当长的, 一个类别的事情基本会放在一篇文章以内, 比如这篇”Simple -> Complex”, 我准备存放的是一些自己对简单结构的思考和想法. 所以今后一篇文章发布出去了仍然会不断的更新, 以保证每篇文章的质量和体系, 以构建自己的知识框架.

几何迭代

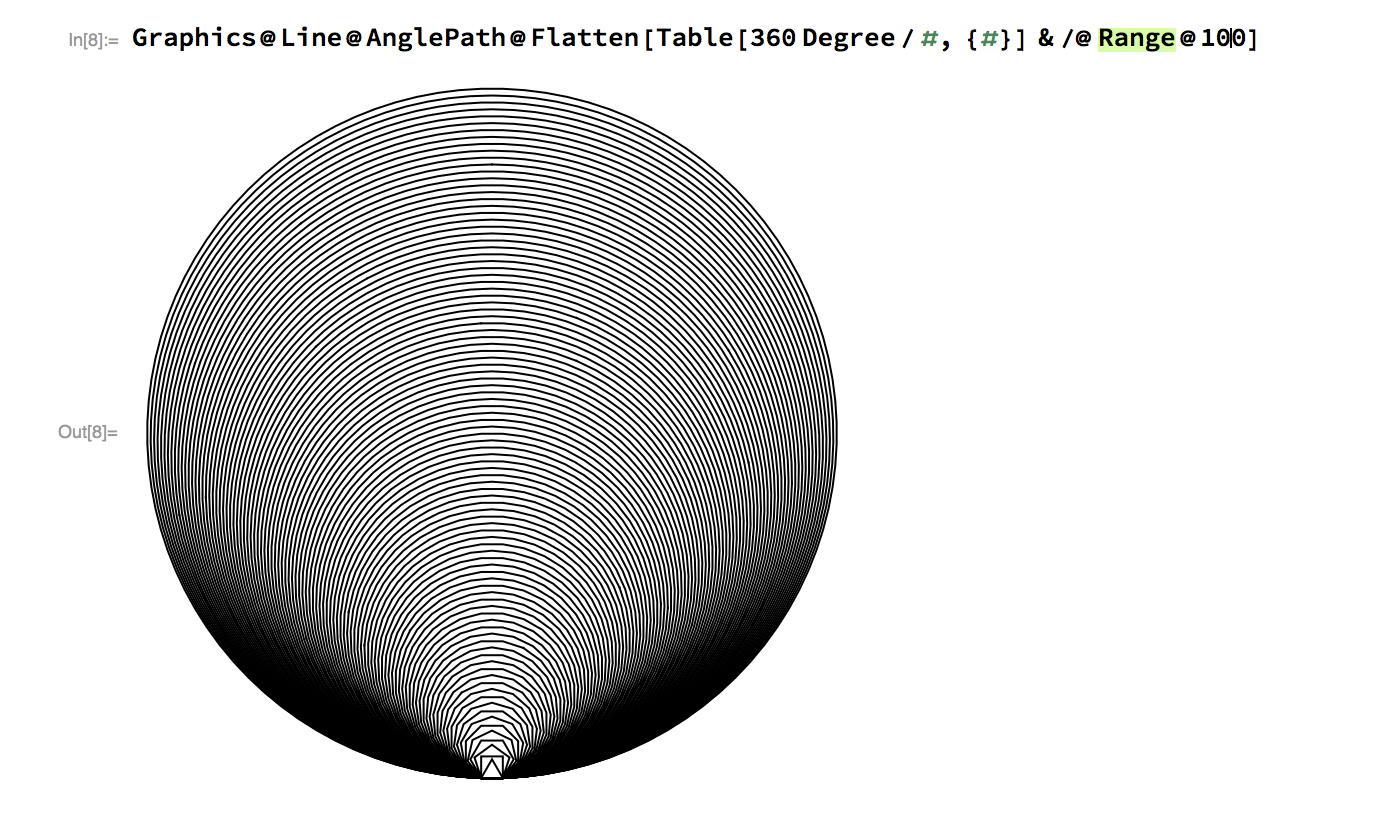
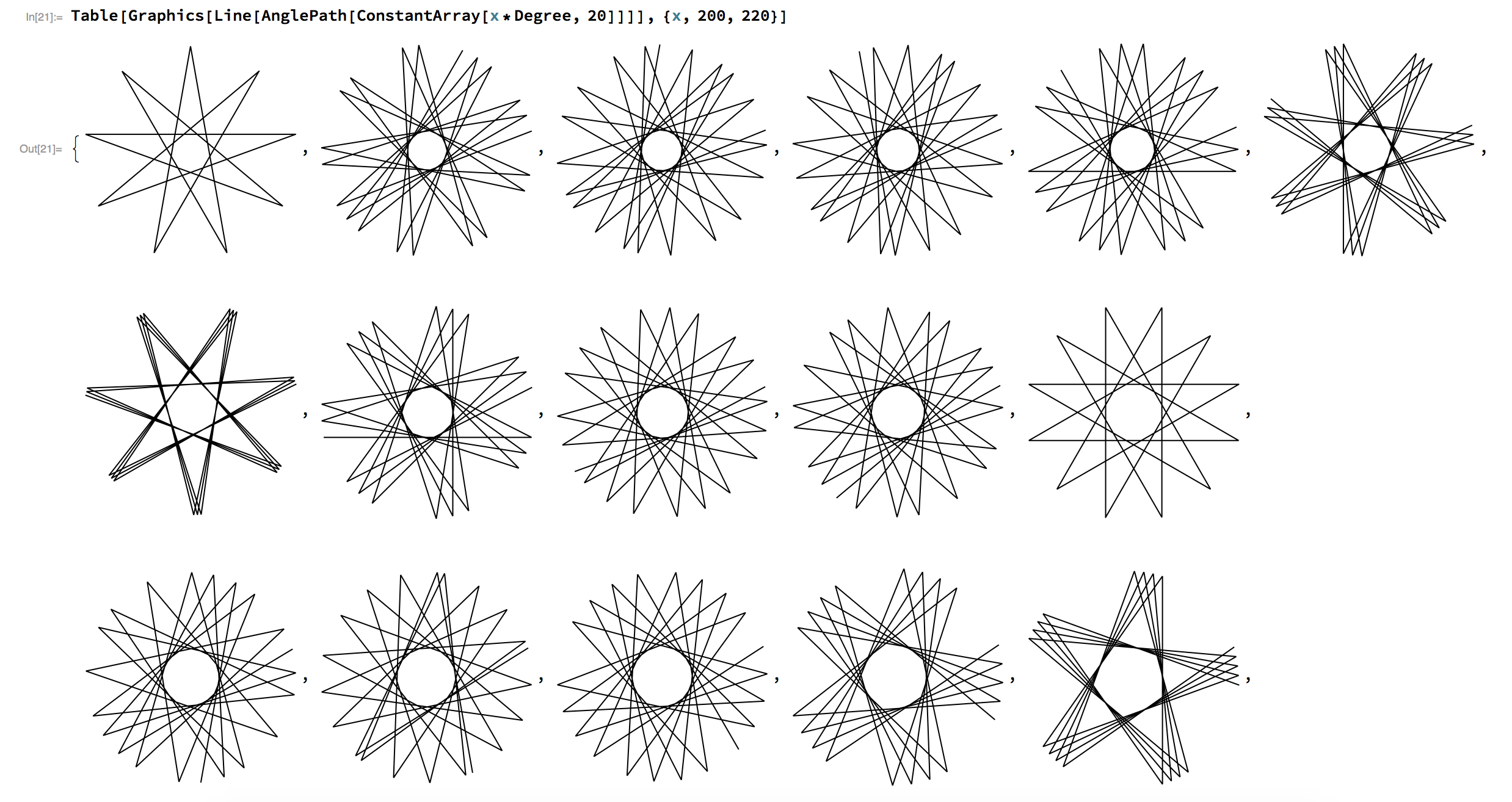
对简单的一个点, 给定一个初始角度, 角度更新规则, 我们可以形成非常多的精妙的图形

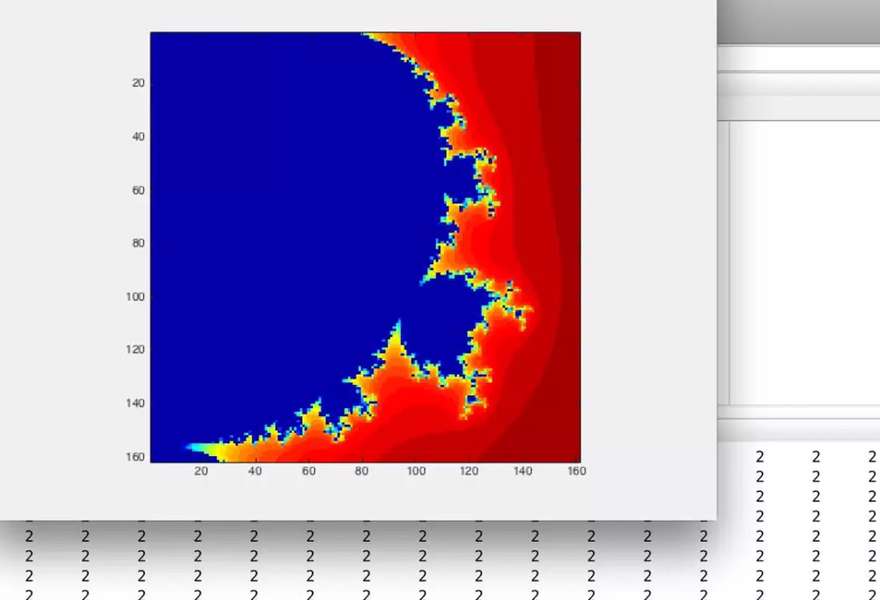
这一点上对分形也是有效的, 分形的原理就是在复数域上的迭代, 设定一定的逃逸半径就可以形成非常精细的分形图像,
在matlab上绘制如下, 这里只取了一定区域的分形, 对分形的进一步讨论建议阅读experiment with matlab这本书, 书上很精妙的讲解和绘制一一些分形局部图形.