关于Euler project.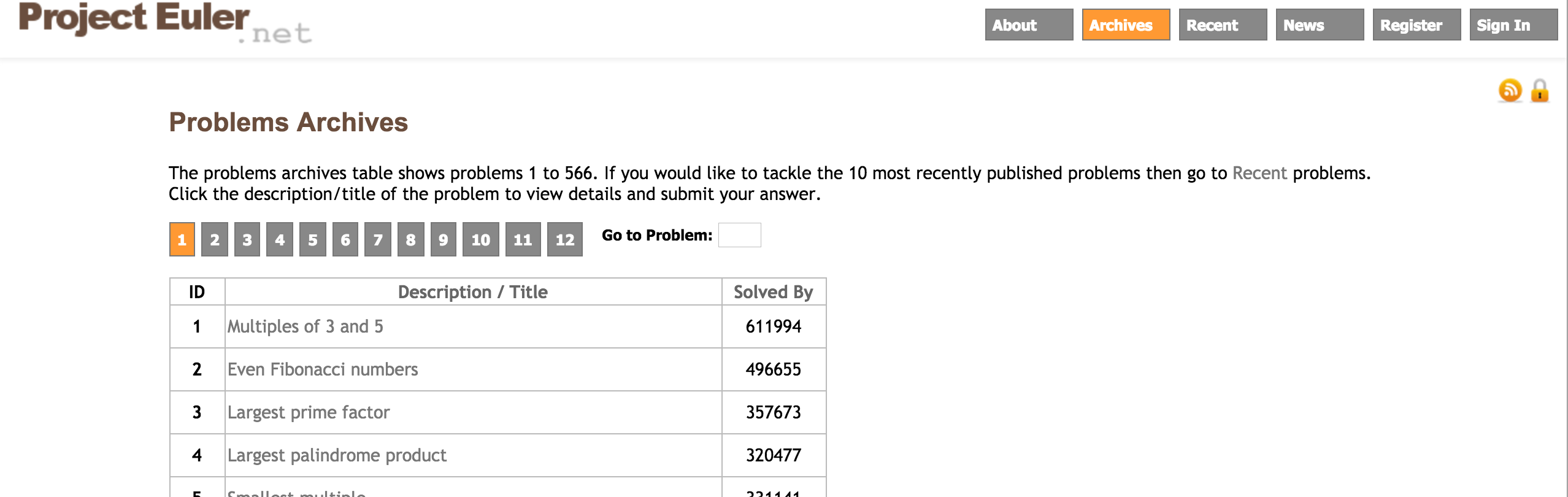

其实之前用mathematica写过几十题, 但是因为mathematica本身语言太高级了, 虽然写起来很方便, 但是自己对内部实现一无所知, 比如Prime[n]函数, 直接给出第n个质数, 这在其他编程语言里都是没有的, 但是这些基本的实现我感觉还是非常重要的.

所以这篇文章, 作为一个练手项目, 准备以三种语言过一遍euler projects, 分别是Haskell, python, c++, 当然因为最近学haskell比较多, 所以可能更新haskell代码比较多.

第一题

If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23.
Find the sum of all the multiples of 3 or 5 below 1000.

solveProblem xs n = sum [i | i <- [1..n],or [i `mod` x == 0| x <- xs]]

main = print $ solveProblem [3,5] 1000

第二题

Each new term in the Fibonacci sequence is generated by adding the previous two terms. By starting with 1 and 2, the first 10 terms will be:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
By considering the terms in the Fibonacci sequence whose values do not exceed four million, find the sum of the even-valued terms.

fib = 1:2:zipWith (+) fib $ tail (fib)

solveProblem n = sum $ filter even $ takeWhile (<n) fib

main = print $ solveProblem 4e6

这里需要注意的是4e6需要指定类型, 一般用floor来指定为Integer…

第三题

The prime factors of 13195 are 5, 7, 13 and 29.
What is the largest prime factor of the number 600851475143 ?

factors x = factorHelper x 2
factorHelper x n | n * n > x = x
                | x `mod` n == 0 = n : factorHelper (x `div` n) n
                | otherwise = factorHelper x n+1
solveProblem n = last $ factors n
main = print $ solveProblem 600851475143

注意一下(:)和(++)的区别, :是prepend, 把单个元素加载list前方, 而++的两个元素都可以为list, :则不行, 所以一般++更通用, 除非可以确定为一个元素, 否则用++, 所以:在模式匹配中更常用, 可以用来提取单个元素!
如

reverse :: [Int] -> [Int]
reverse (x:xs) = reverse xs ++ x

: conses an element onto a list.
++ appends two lists.
The former has type
a -> [a] -> [a]
whereas the latter has type
[a] -> [a] -> [a]

第四题

准备写一下欧拉计划的题解.
Project Eular

前面10题比较简单 就不写了, 秒过= =

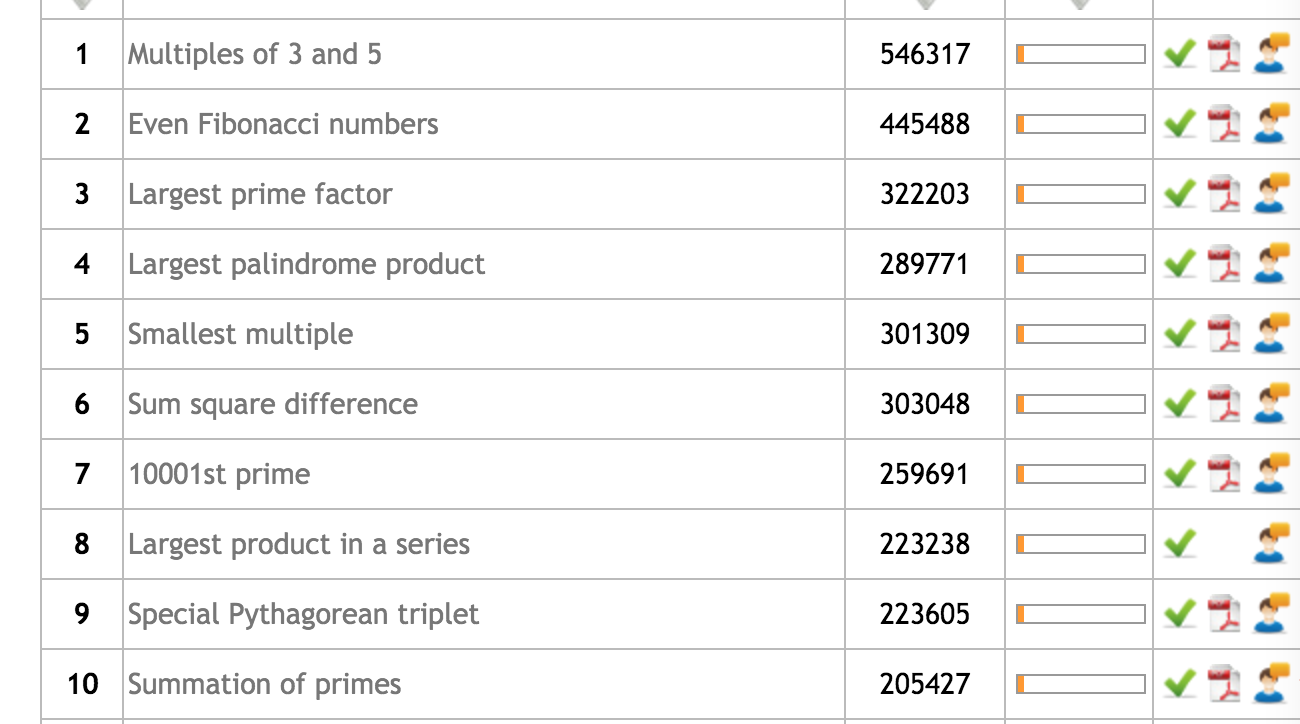
跳到了45题开始做
…

45 和48貌似算法效率有点低.. 跑两分钟还没出来就abort掉了 准备晚上挂着跑 = = 先写这么多题解吧.

可以从50题开始刷了.

46题

It was proposed by Christian Goldbach that every odd composite number can be written as the sum of a prime and twice a square.

9 = 7 + 2×12
15 = 7 + 2×22
21 = 3 + 2×32
25 = 7 + 2×32
27 = 19 + 2×22
33 = 31 + 2×12

It turns out that the conjecture was false.

What is the smallest odd composite that cannot be written as the sum of a prime and twice a square?

isSquare[x_] := IntegerQ[x/2] && IntegerQ[Sqrt[x/2]]
isnotConjecture[x_] := 
 If[Select[
    Table[isSquare[x - Prime[i]], {i, 1, 
      NestWhile[1 + # &, 1, Prime[#] <= x &] - 1}], # == 
      True &] == {}, x, 0]
Select[isnotConjecture /@ Table[i, {i, 3, 6000, 2}], # != 0 &]//First

答案5777

47题

The first two consecutive numbers to have two distinct prime factors are:

14 = 2 × 7
15 = 3 × 5

The first three consecutive numbers to have three distinct prime factors are:

644 = 2² × 7 × 23
645 = 3 × 5 × 43
646 = 2 × 17 × 19.

Find the first four consecutive integers to have four distinct prime factors. What is the first of these numbers?

Times @@ Power @@@ (Select[
      FactorInteger /@ 
       Table[{i, i + 1, i + 2, i + 3}, {i, 1000, 1000000}], 
      Length[#[[1]]] == Length[#[[2]]] == Length[#[[3]]] ==Length[#[[4]]] == 4 &] // First)[[1]]

答案134043

48题

The series, 1^1 + 2^2 + 3^3 + … + 10^10 = 10405071317.

Find the last ten digits of the series, 1^1 + 2^2 + 3^3 + … + 1000^1000.

Sum[Reverse[ToExpression[Characters[ToString[Sum[i^i, {i, 1, 1000}]]]]][[k]]*10^(k - 1), {k, 1, 10}]

答案9110846700

50题

The prime 41, can be written as the sum of six consecutive primes:

41 = 2 + 3 + 5 + 7 + 11 + 13
This is the longest sum of consecutive primes that adds to a prime below one-hundred.

The longest sum of consecutive primes below one-thousand that adds to a prime, contains 21 terms, and is equal to 953.

Which prime, below one-million, can be written as the sum of the most consecutive primes?

Select[Flatten[
   Table[Sum[Prime[i], {i, k, j}], {k, 2, 
     NestWhile[# + 1 &, 1, Sum[Prime[k], {k, 1, #}] < 1000000 &] - 
      1}, {j, k + 1, 
     NestWhile[# + 1 &, 1, Sum[Prime[k], {k, 1, #}] < 1000000 &] - 
      1}]], PrimeQ] // Max

997651

话说图床老是挂…传个图好麻烦.

最近找到一个sm.ms还行