今天整理了下电脑上的PDF, 看到了一篇关于cycloid的文章, 看了下貌似是之前下的忘记看了, 就看了一下, 结果发现很有意思, 是关于Brachistochrone curve, 即最速曲线的一篇论文, 其实际上是由摆线形成的.


至于摆线, 维基上的解释是A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line without slippage. It is an example of a roulette, a curve generated by a curve rolling on another curve.

其性质非常多, 最著名的自然就是两点

1. 最速降线
2. 在其形成的容器上, 不管在任何一点上放下, 其最后落在中间的时间是相同的.

而我看的那篇文章就是证明这个摆线是两点间的最速降线的一片文章.

最速降线实际的效果如下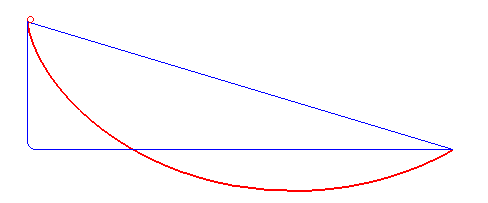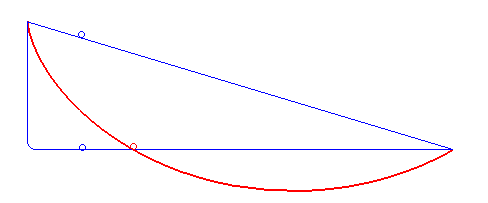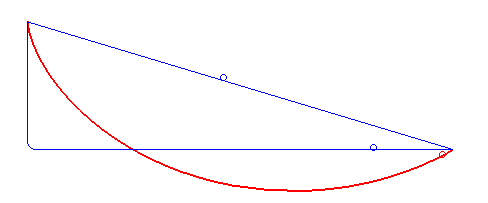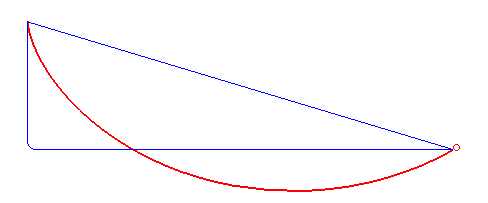

在这条曲线下, 物体下降到达目标地点的速度是最快的.
证明过程不在赘述, 最后可以通过能量守恒和积分把下降时间作为目标函数写出如下$$T=\int_0^x\sqrt{\frac{1+{y’}^2}{2gy}}dx$$
这个形式很容易就可以想到eular-lagrange方程, 其主要就是用来解这种定积分的优化问题, 我们将$\sqrt{\frac{1+{y’}^2}{2gy}}$改写成$L(x,y,y’)$, 那么我们目标就是找到这样一个$y$, 使得T最小.

eular-lagrange方程如下
$$L_x(t,q(t),q’(t))-\frac{d}{dt}L_v(t,q(t),q’(t))=0$$
这个方程的解就是我们要求的y.

解出这个方程, 我们就有了摆线方程$$x=r(t-sint)$$$$y=r(1-cost)$$
其中$t\in(0,2\pi)$