optimization models and its application笔记1-线性代数
内容为optimization models and its application这本书的笔记, 内容非常好, 复习了一下线代和凸优化. 这里是第一章的笔记, 关于线性代数, 感觉自己线代确实学的还是挺水的…不知其所以然. 这本书会从motivation开始讲起, 每篇开头都是the goal of …., 从意义开始讲, 公式推导的部分较少, intuition上的解释更多.
1 矩阵
正定矩阵(Orthogonal matrices)
$U^TU=I_n$
一般来说可以说非奇异矩阵就是正定矩阵, 其逆等于其矩阵的转置
其特征为
- 映射$x->Ux$后, x将保持长度不变, 改变的是角度.
- x,y同时变化后, 其相对角度不变.
枚举矩阵
对形式为单位矩阵的枚举, 可以用来对一组数进行枚举.
Dyads
Dyads are a special class of matrices, also called rank-one matrices, for reasons seen later.
其秩恒为1, 由于其可以分解为$A=uv^T$
所以有$Ax=(uv^T)x=(v^Tx)u$
从映射的角度来看, $x$在映射后不管怎么样将会保持与u相同的角度, 其扩张的程度取决于$v$
有一个例子是对不同资产的增长额, 其行为时间, 列为不同的资产类型, 这里按照dyads进行分解, 可以对每一种资产进行其与时间线性近似, 似乎就是一种线性回归吧.
QR分解
解释为The basic goal of the QR decomposition is to factor a matrix as a product of two matrices (traditionally called $Q$,$R$, hence the name of this factorization). Each matrix has a simple structurewhich can be further exploited in dealing with, say, linear equations.
即作用是用两个简单的矩阵代替原矩阵, 进而对矩阵进行求解.
matlab代码如下
[Q,R] = qr(A,0); % A is a mxn matrix,
%Q is mxn orthogonal, R is nxn upper triangular
对全QR分解
[Q,R] = qr(A);%Q is mxm orthogonal, R is mxn upper triangular
可以通过观察R的rank来观察A的rank.
线性映射
对一个$m{\times}m$矩阵$A$, 可以把A看做一个线性映射$f:R^n->R^m$, 即$f(x)=Ax$, 反过来看, 对每一个线性映射, 我们都可以找到这样一个f, 来使得$f(x)=Ax$
对于仿射, 有对$f(x)=Ax+b$, 当 $ b = 0$的时候该仿射为线性映射.
解释上这样理解, $A_{ij}$为$x_j$对$yi$的影响程度. 因此, 如果$A{13} >> A_{14}$, 则可以认为$x_3$比起$x_4$对$y1$有更大的影响力, 或者, 当$A{24}=0$时说$y_4$对$x_2$的影响程度为0, 其值不依靠$x_2$来影响, 通常来说, $b=f(0)$被看作偏置(bias).
非线性映射的一阶线性近似. 其方法为泰勒展开的一阶展开, 对非线性映射
$$R^n->R^m$$, 若其是可微的, 对其的线性近似形式 为
$$f(x){\approx}\dot f=f(x_0)+A(x-x0)$$
这里的
$$A{ij}=\frac{\partial y_i}{\partial x_j}(x_0)$$, 这里记忆可以理解为在利用函数在$x_0$上的值与其导数进行一阶线性近似, 同时$A$为$f$在$x_0$处的$jacobian$矩阵.
标注一下, 这里的jacobian矩阵原来和线性映射及泰勒展开是紧密相连的, 以前确实没有想到这一点, 感觉茅塞顿开啊…, 不过由于是一阶近似, 其形式只能在展开点$x_0$附近处使用.
矩阵范数
Motivation
对一个音频输入$x$, 其存在噪声, 讨论其噪声对输出的平均影响和最大影响.
对于平均影响, 有
RMS gain (root-mean-square) : the Frobenius norm
其值可以用弗罗贝尼乌斯范数(Frobenius norm)来计算,
公式为
$$||A||F :=\sqrt{\sum{i=1}^{m}\sum{j=1}^nA^{2}{ij}}=\sqrt{Tr(A^TA)}$$
matlab中可以写作
norm(A,'fro');
对于最大影响
对$v$如果有$||v||2\leq \alpha$, 那么有如下的定义
Largest singular value norm.: An alternate way to measure matrix size is based on asking the maximum ratio of the norm of the output to the norm of the input. When the norm used is the Euclidean norm, the corresponding quantity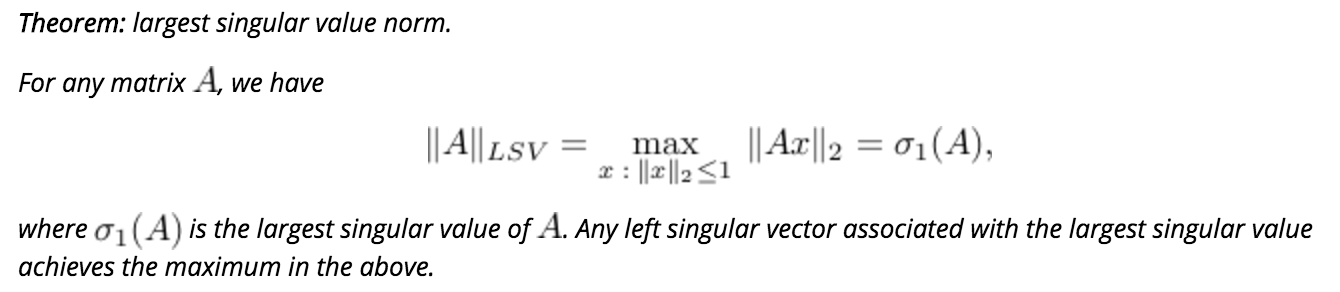
即$$||A||{LSV}$$的值等于矩阵$A$的最大的一个奇异值的值.
matlab中计算可以用
lsv_norm = norm(A);
就是矩阵的范数, 其值等于最大的奇异值.
应用矩阵间的距离
同样可以使用上面两种范数进行计算, 一种弗罗贝尼乌斯范数, 一种矩阵范数(其值就是最大的奇异值), 解释为一个是平均差距, 一个是最大差距.
最大方差投影方向
Let us try to visualize the data set by projecting it on a single line passing through the origin. The line is thus defined by a vector$x\in R^m$ , which we can without loss of generality assume to be of Euclidean norm . The data points, when projected on the line, are turned into real numbers$x^Ta_i,i=1,…,n$ .
It can be argued that a good line to project data on is one which spreads the numbers$x^Ta_i$ as much as possible. (If all the data points are projected to numbers that are very close, we will not see anything, as all data points will collapse to close locations.)
就不翻译了, 这里需要找到一个投影方向使得$a_i$在该方向的投影上的各个值方差最大, 本身也是一个优化问题, 其值可以用最大奇异值来计算, 即LSV范数.
条件数(condition number)
Condition number.:The condition number of an invertible matrix is the ratio between the largest and the smallest singular values
定义为最大的奇异值与最小奇异值的比值,
$$k(A)=\frac{\sigma_1}{\sigma_n}=||A|| \times ||A^{-1}||$$
其解释为线性方程组A的解的敏感度.
2 线性方程组
Motivation
这里的例子非常有意思, 对于医疗上的CAT(Computerized Axial Tomography), 其的重构实际上就是一个线性方程组的解得唯一性问题.


用X光可以获得的是一束x光从一个方向穿透过去后光强的下降比例, 那么将X光在统一切片上的不同方向进行发射, 可以获得很多组比例信息.
对于y, 有公式
$$y=log\frac{I{rec}}{I{source}}=\sum{(i,j)\in T}A{ij}d_{ij}$$
原理如下, 对于需要重构的密度信息矩阵如下
从不同的方向发射x光, 获得y
那么对于上面的例子, 我们可以得到线性方程组,
接下来就需要讨论其解得唯一性(unicity)与存在性(existence), 因为我们需要一个确定的$X$矩阵来对大脑切边进行CAT重构.实际上可以看到的是, 一般来说列的数目都要远小于行的数目, 这是由于x光发射的数目远小于密度矩阵的单元个数, 所以这样的矩阵一般来说都是解不唯一的.