牛顿法

目前来看, 牛顿法主要的用处有两个

1. 函数的寻根

并不是所有的方程都有求根公式, 或者求根公式很复杂, 导致求解困难. 利用牛顿法, 可以迭代求解.

原理是利用泰勒公式, 在$x_0$处泰勒展开, 且展开到一阶, $f(x)=f(x_0)+(x-x_0)f’(x_0)$.

求解$f(x)=0$, 既$f(x_0)+(x-x_0)f’(x_0)=0$, 就可以推出$x=x_1=x_0-f(x_0)/f’(x_0)$, 当然由于是泰勒一阶展开, 后面很多的项都省略了, 所以有一点的误差, 其近似过程如下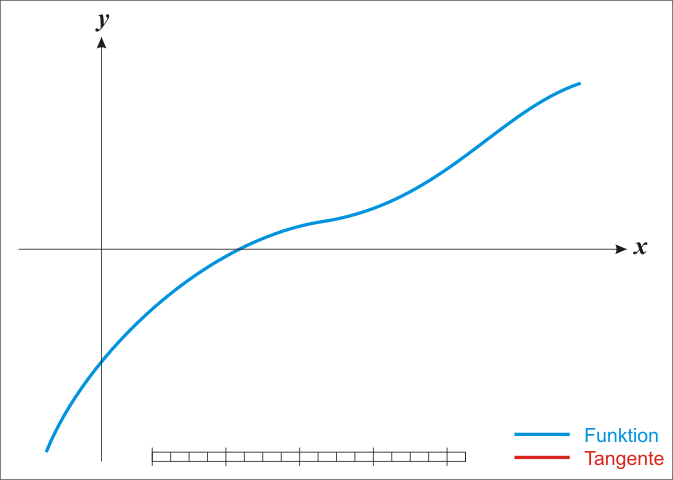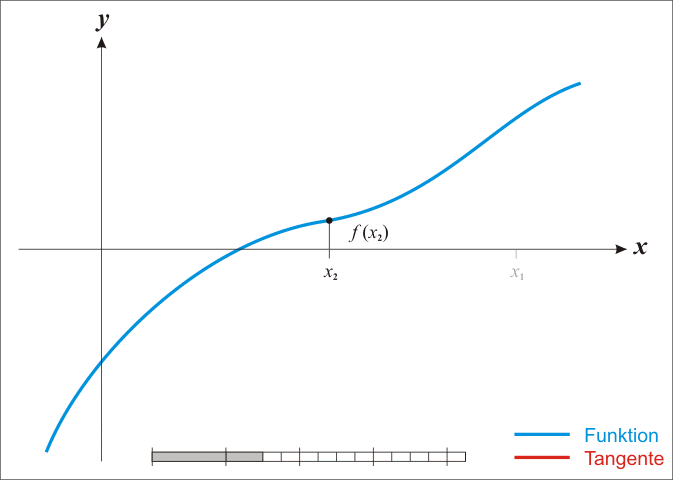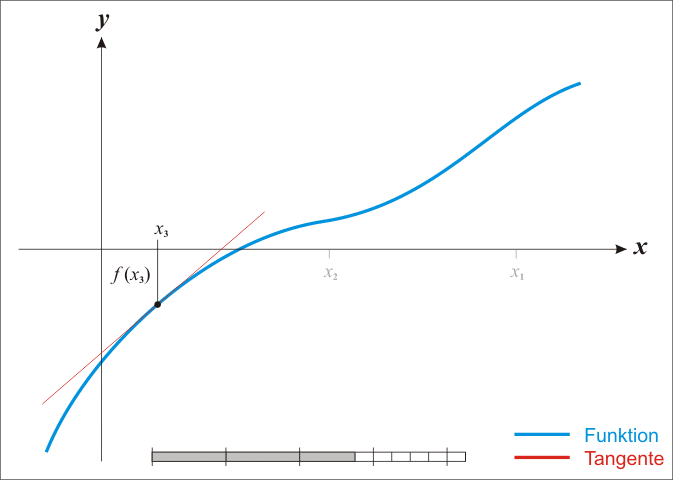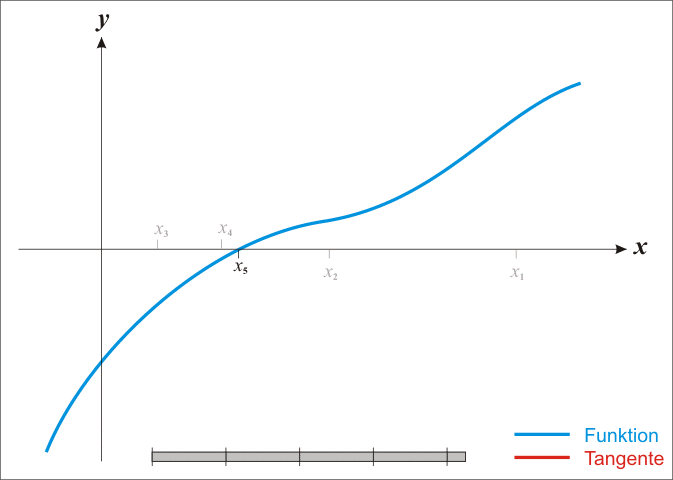

下面举个例子, 我们考虑下面这个二元函数组.
$$\begin{equation}\left{\begin{aligned}x^2+y^2-5=0 \(x+1)y-3y-1=0\\end{aligned}\right.\end{equation}$$
那么用牛顿法求解的R代码可以如下这样写.

f1<-function(x){  
    f<-c(x[1]^2+x[2]^2-5,(x[1]+1)*x[2]-3*x[1]-1)  
    j<-matrix(c(2*x[1],2*x[2],x[2]-3,x[1]+1),2,2,byrow=T)  
    list(f=f,j=j)  
}  


fnewton<-function(f1,x,eps=1e-5){  
    repeat{  
        x1<-x  
        object<-f1(x)  
        x<-x-solve(object$j,object$f)  
        if((x-x1)%*%(x-x1)

2. 最优化

其实原理和寻根一样, 不同的是求的是导数的根, 这时候问题就在于多元函数的二阶导数形成的hessian矩阵比较大, 也就是计算量很大, 所以有伪牛顿法等方法, 用一些办法来近似这个hessian矩阵, 以快速迭代, 当然这个hessian矩阵, 可以在mathematica直接用D函数进行求解, 具体公式就不推导了.

作为一个例子, 多变量函数的优化求解的牛顿法的mathematica代码如下, 需要注意的是需要首先求出这个多变量函数的雅克比式, 然后在进行hessian矩阵的求解, 之后进行迭代, 这里的迭代和least square也是息息相关的.

f[{x_, y_, z_}] = {x - Sin[y], z - Cos[y], Cos[x] Sin[z]};
J[{x_, y_, z_}] = D[f[{x, y, z}], {{x, y, z}}];
FixedPoint[(# - LinearSolve[J[#], f[#]]) &, {.5, .5, .5}]

一般认为牛顿法可以利用到曲线本身的信息, 比梯度下降法更容易收敛（迭代更少次数）, 如下图是一个最小化一个目标方程的例子, 红色曲线是利用牛顿法迭代求解, 绿色曲线是利用梯度下降法求解.

另外可以看到不管怎么样都需要一个初始点进行迭代, 点的选取对于迭代的结果影响比较大, 不得不说1stopt这个软件有点黑魔法…不知道怎么弄的初始点, 有点想到他们公司实习实习了…