图论高级算法及实现

现在对一个图主要的计算基本有

哈密顿回路
TSP
postman
欧拉图
最大流
最小花费最大流

下面做实例

练习同时做保存

最大流

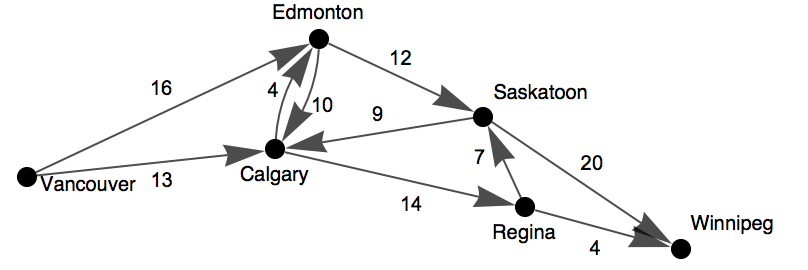
Based on a 1940 Soviet railway network, find the maximum amount of cargo that can be transported from sources in the Western Soviet Union to destinations in Eastern European countries.

eg:

原始图

data= 
  FindMaximumFlow[g, "Vancouver", "Winnipeg", "OptimumFlowData"];

  Grid[{#, data[#]} & /@ \[ScriptCapitalF]["EdgeList"],Frame -> All, Alignment -> Left]

 makelabels[railway_, data_] := 
  Block[{edgecap = EdgeCapacity /. Options[railway, EdgeCapacity]}, 
   Map[(# -> 
       Framed[Style[
         Row[{edgecap[[EdgeIndex[railway, #]]], "/", data[#]}], 
         Directive[8.2, FontFamily -> "Helvetica"]], 
        FrameMargins -> {{-.2, -.2}, {-.7, -.7}}, 
        Background -> GrayLevel[.9], FrameStyle -> None]) &, 
    data["EdgeList"]]];


SetProperty[\[ScriptCapitalF][
  "FlowGraph"], {EdgeLabels -> makelabels[g, \[ScriptCapitalF]]}]

maxflow matrix

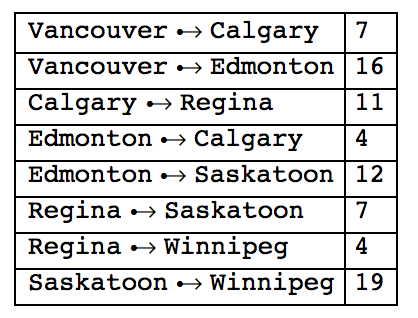
maxflow graph

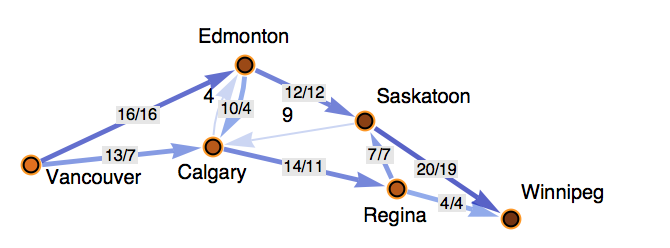
哈密顿回路

以一个简单有向最短路为例

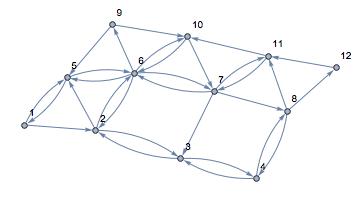
data = SparseArray[{{1, 2} -> 150, {1, 5} -> 165, {2, 3} -> 
     130, {2, 5} -> 230, {2, 6} -> 160, {3, 2} -> 140, {3, 4} -> 
     100, {4, 3} -> 100, {4, 8} -> 190, {5, 1} -> 165, {5, 6} -> 
     144, {6, 2} -> 170, {6, 5} -> 144, {6, 7} -> 128, {6, 9} -> 
     218, {6, 10} -> 174, {7, 3} -> 200, {7, 6} -> 122, {7, 8} -> 
     109, {7, 11} -> 185, {8, 4} -> 180, {8, 11} -> 141, {8, 12} -> 
     190, {9, 10} -> 148, {9, 5} -> 194, {10, 6} -> 174, {10, 7} -> 
     233, {11, 7} -> 185, {11, 10} -> 135, {12, 11} -> 110}, {12, 12},
    Infinity] // Normal
graph = WeightedAdjacencyGraph[data, VertexLabels -> "Name"]

one answer

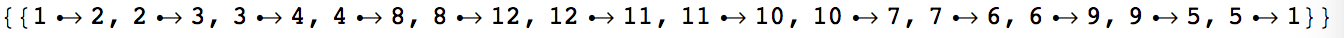
稀疏矩阵生成有向图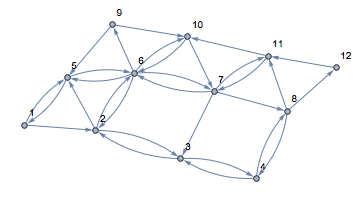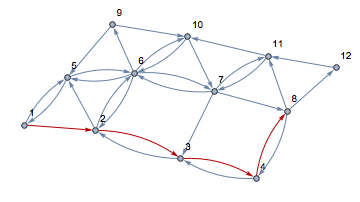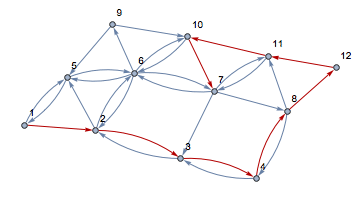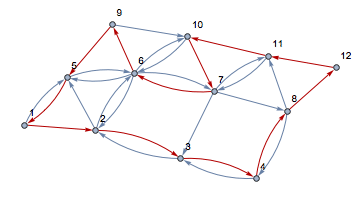

ans1 = FindHamiltonianCycle[graph, All]
Table[HighlightGraph[graph, ans1[[1, 1 ;; i]]], {i, 0, 
  Length[ans1[[1]]]}]

postman

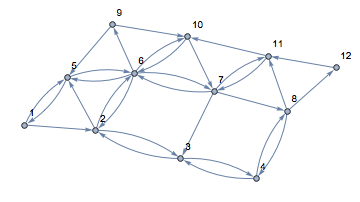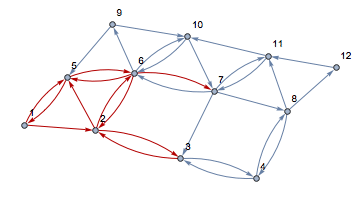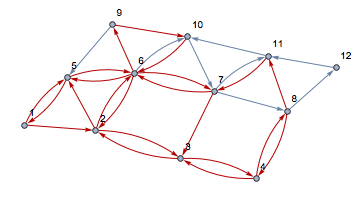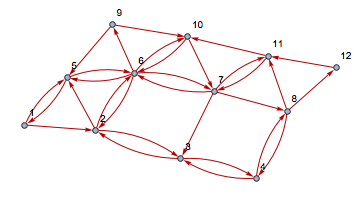
ans1 = FindPostmanTour[graph]
Table[HighlightGraph[graph, ans1[[1, 1 ;; i]]], {i, 0, 
  Length[ans1[[1]]]}]

印度地图的一个postman

图片貌似出问题了…

下次补充吧

TSP

类似

不再赘述

用FindShortestTour

单源最短路等可以用FindShortestPath

其中参数可以用All.

余下慢慢补充(大雾)(PS… 感觉写并且总结这些也挺花功夫的= =..还有好多今天写的没有写上来以后熟练点应该会好点吧))