常微分方程与旋转图
想着来个大新闻 所以今天晚上把这几天的存货都发了好吧其实是我懒
今天看到一个有意思的题目.大概意思是兔子在狼的正西方100米处,兔子的窝在其正北50m处,当t=0时狼开始追兔子并且兔子开始逃跑,问能否追到兔子
明显解微分方程题目
mathematica 代码如下
a = NDSolve[{x'[t] ==
2*(-100 - x[t])/Sqrt[(-100 - x[t])^2 + (t - y[t])^2],
y'[t] == 2*(t - y[t])/Sqrt[(-100 - x[t])^2 + (t - y[t])^2],
x[0] == 0, y[0] == 0}, {x[t], y[t]}, {t, 0, 66.68}];
ParametricPlot[{{x[t] /. a // First, y[t] /. a // First}, {-100,
t}}, {t, 0, 66.68}, PlotRange -> All]
…
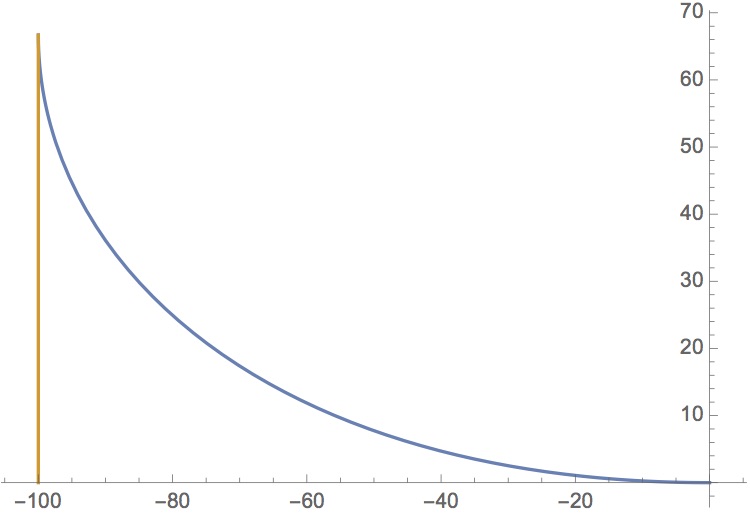
蓝线为狼的轨迹, 橙线为兔子轨迹
显然追上时y超过50 兔子已经安全逃离
类似一个虫子的题目,有个边长为a的正方形ABCD,四个顶点有四只虫子,由初始位置出发,A追B,B追C,C追D,D追A,运动速度的大小均为v,问最后他们走过的路程。
a = NDSolve[{(x2[t] - x1[t]) ==
x1'[t] Sqrt[(x2[t] - x1[t])^2 + (y2[t] - y1[t])^2], (y2[t] -
y1[t]) ==
y1'[t] Sqrt[(x2[t] - x1[t])^2 + (y2[t] - y1[t])^2], (x3[t] -
x2[t]) ==
x2'[t] Sqrt[(x3[t] - x2[t])^2 + (y3[t] - y2[t])^2], (y3[t] -
y2[t]) ==
y2'[t] Sqrt[(x3[t] - x2[t])^2 + (y3[t] - y2[t])^2], (x4[t] -
x3[t]) ==
x3'[t] Sqrt[(x4[t] - x3[t])^2 + (y4[t] - y3[t])^2], (y4[t] -
y3[t]) ==
y3'[t] Sqrt[(x4[t] - x3[t])^2 + (y4[t] - y3[t])^2], (x1[t] -
x4[t]) ==
x4'[t] Sqrt[(x1[t] - x4[t])^2 + (y1[t] - y4[t])^2], (y1[t] -
y4[t]) == y4'[t] Sqrt[(x1[t] - x4[t])^2 + (y1[t] - y4[t])^2],
x1[0] == 1, y1[0] == 1, x2[0] == 1, y2[0] == 0, x3[0] == 0,
y3[0] == 0, x4[0] == 0, y4[0] == 1}, {x1[t], y1[t], x2[t], y2[t],
x3[t], y3[t], x4[t], y4[t]}, {t, 0, 1}]
ParametricPlot[{{First@(x1[t] /. a),
First@(y1[t] /. a)}, {First@(x2[t] /. a),
First@(y2[t] /. a)}, {First@(x3[t] /. a),
First@(y3[t] /. a)}, {First@(x4[t] /. a), First@(y4[t] /. a)}}, {t,
0, 1}, PlotRange -> All]
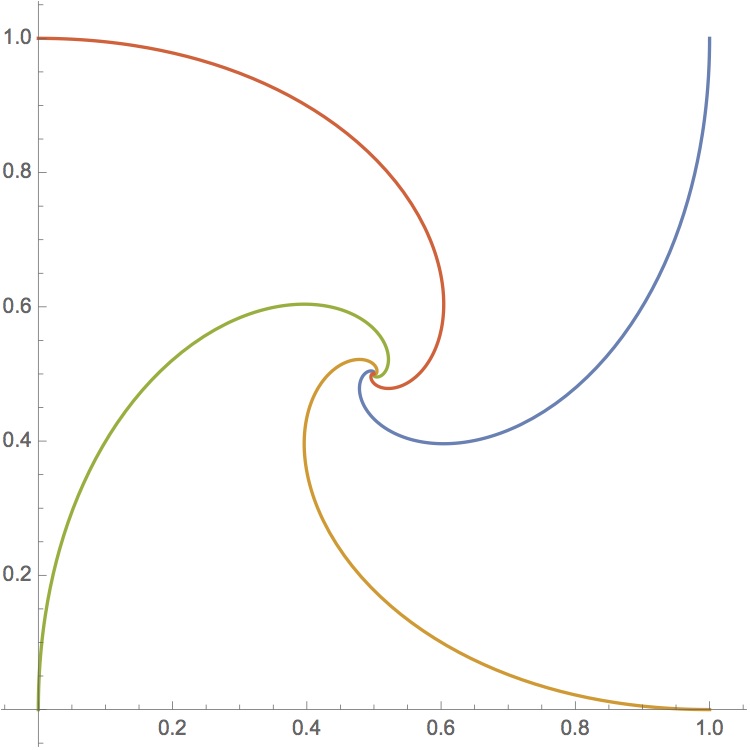
四虫轨迹.
mathematica大法好!!
另外….前些天写的没有更上来的也写上来
一个画旋转图形
我们知道对一个
x^2 + (-2 + y)^2 == 1
的式子 要求其对X轴旋转一周的图形
只需要把Y变换为Sqrt[y^2 + z^2]
所以有了x^2 + (-2 + Sqrt[y^2 + z^2])^2 == 1
于是对这样的函数可以直接用contourplot3d来画
ContourPlot3D[
x^2 + (-2 + (y^2 + z^2)^(1/2))^2 == 1, {x, -Pi, Pi}, {y, -Pi,
Pi}, {z, -Pi, Pi}]
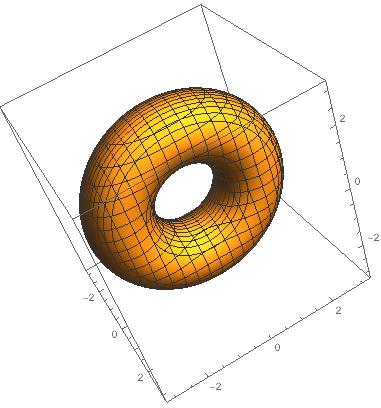
这样画似乎不太好看 用区间画法
DiscretizeRegion@
ImplicitRegion[x^2 + (-2 + (y^2 + z^2)^(1/2))^2 == 1, {x, y, z}]
软绵绵的麦圈…
最后对于旋转图像有一个特定的函数revolutionplot3D
RevolutionPlot3D[{Cos[t] + 2, Sin[t]}, {t, 0, 2 Pi}]
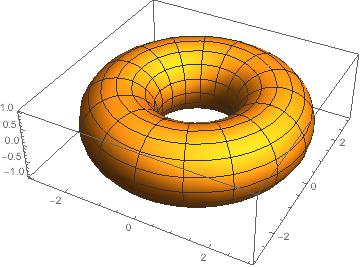
话说最近写的都是用mathematica, 对matlab确实无感啊= = 一些参数太复杂看不动…用了过几天就忘记了.
python也可以 但是现在用的还不熟, 一些函数还是mathematica好用.
现在基本python可以代替C++使用了,好用的多.